

The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
This R package is for high-dimensional multivariate Bayesian variable
and covariance selection in linear regression, including methods in Bottolo et al. (2021), Zhao et al. (2021) and
Zhao et al. (2024).
See the package vignettes BayesSUR.pdf for more
information and an additional example below for the BayesSUR model with
random effects.
Install the latest released version from CRAN
install.packages("BayesSUR")Install the latest development version from GitHub
#install.packages("remotes")
remotes::install_github("mbant/BayesSUR/BayesSUR")The BayesSUR model has been extended to include mandatory variables by assigning Gaussian priors as random effects rather than spike-and-slab priors, named as SSUR-MRF with random effects in Zhao et al. 2023. The R code for the simulated data and real data analyses in Zhao et al. 2023 can be found at the GitHub repository BayesSUR-RE.
Here, we show a simulation example to run the BayesSUR mdoel with random effects.
We design a network as the following figure (a) to construct a complex structure between \(20\) response variables and \(300\) predictors. It assumes that the responses are divided into six groups, and the first \(120\) predictors are divided into nine groups.

Figure: True relationships between response variables and predictors. (a) Network structure between \(\mathbf Y\) and \(\mathbf X\). (b) Spare latent indicator variable \(\Gamma\) for the associations between \(\mathbf Y\) and \(\mathbf X\) in the SUR model. Black blocks indicate nonzero coefficients and white blocks indicate zero coefficients. (c) Additional structure in the residual covariance matrix between response variables not explained by \(\mathbf X\mathbf B\). Black blocks indicate correlated residuals of the corresponding response variables and white blocks indicate uncorrelated residuals of the corresponding response variables.
Load the simulation function sim.ssur() as follows.
sim.ssur <- function(n, s, p, t0 = 0, seed = 123, mv = TRUE,
t.df = Inf, random.intercept = 0, intercept = TRUE) {
# set seed to fix coefficients
set.seed(7193)
sd_b <- 1
mu_b <- 1
b <- matrix(rnorm((p + ifelse(t0 == 0, 1, 0)) * s, mu_b, sd_b), p + ifelse(t0 == 0, 1, 0), s)
# design groups and pathways of Gamma matrix
gamma <- matrix(FALSE, p + ifelse(t0 == 0, 1, 0), s)
if (t0 == 0) gamma[1, ] <- TRUE
gamma[2:6 - ifelse(t0 == 0, 0, 1), 1:5] <- TRUE
gamma[11:21 - ifelse(t0 == 0, 0, 1), 6:12] <- TRUE
gamma[31:51 - ifelse(t0 == 0, 0, 1), 1:5] <- TRUE
gamma[31:51 - ifelse(t0 == 0, 0, 1), 13:15] <- TRUE
gamma[52:61 - ifelse(t0 == 0, 0, 1), 1:12] <- TRUE
gamma[71:91 - ifelse(t0 == 0, 0, 1), 6:15] <- TRUE
gamma[111:121 - ifelse(t0 == 0, 0, 1), 1:15] <- TRUE
gamma[122 - ifelse(t0 == 0, 0, 1), 16:18] <- TRUE
gamma[123 - ifelse(t0 == 0, 0, 1), 19] <- TRUE
gamma[124 - ifelse(t0 == 0, 0, 1), 20] <- TRUE
G_kron <- matrix(0, s * p, s * p)
G_m <- bdiag(matrix(1, ncol = 5, nrow = 5),
matrix(1, ncol = 7, nrow = 7),
matrix(1, ncol = 8, nrow = 8))
G_p <- bdiag(matrix(1, ncol = 5, nrow = 5), diag(3),
matrix(1, ncol = 11, nrow = 11), diag(9),
matrix(1, ncol = 21, nrow = 21),
matrix(1, ncol = 10, nrow = 10), diag(9),
matrix(1, ncol = 21, nrow = 21), diag(19),
matrix(1, ncol = 11, nrow = 11), diag(181))
G_kron <- kronecker(G_m, G_p)
combn11 <- combn(rep((1:5 - 1) * p, each = length(1:5)) +
rep(1:5, times = length(1:5)), 2)
combn12 <- combn(rep((1:5 - 1) * p, each = length(30:60)) +
rep(30:60, times = length(1:5)), 2)
combn13 <- combn(rep((1:5 - 1) * p, each = length(110:120)) +
rep(110:120, times = length(1:5)), 2)
combn21 <- combn(rep((6:12 - 1) * p, each = length(10:20)) +
rep(10:20, times = length(6:12)), 2)
combn22 <- combn(rep((6:12 - 1) * p, each = length(51:60)) +
rep(51:60, times = length(6:12)), 2)
combn23 <- combn(rep((6:12 - 1) * p, each = length(70:90)) +
rep(70:90, times = length(6:12)), 2)
combn24 <- combn(rep((6:12 - 1) * p, each = length(110:120)) +
rep(110:120, times = length(6:12)), 2)
combn31 <- combn(rep((13:15 - 1) * p, each = length(30:50)) +
rep(30:50, times = length(13:15)), 2)
combn32 <- combn(rep((13:15 - 1) * p, each = length(70:90)) +
rep(70:90, times = length(13:15)), 2)
combn33 <- combn(rep((13:15 - 1) * p, each = length(110:120)) +
rep(110:120, times = length(13:15)), 2)
combn4 <- combn(rep((16:18 - 1) * p, each = length(121)) +
rep(121, times = length(16:18)), 2)
combn5 <- matrix(rep((19 - 1) * p, each = length(122)) +
rep(122, times = length(19)), nrow = 1, ncol = 2)
combn6 <- matrix(rep((20 - 1) * p, each = length(123)) +
rep(123, times = length(20)), nrow = 1, ncol = 2)
combnAll <- rbind(t(combn11), t(combn12), t(combn13),
t(combn21), t(combn22), t(combn23), t(combn24),
t(combn31), t(combn32), t(combn33),
t(combn4), combn5, combn6)
set.seed(seed + 7284)
sd_x <- 1
x <- matrix(rnorm(n * p, 0, sd_x), n, p)
if (t0 == 0 & intercept) x <- cbind(rep(1, n), x)
if (!intercept) {
gamma <- gamma[-1, ]
b <- b[-1, ]
}
xb <- matrix(NA, n, s)
if (mv) {
for (i in 1:s) {
if (sum(gamma[, i]) >= 1) {
if (sum(gamma[, i]) == 1) {
xb[, i] <- x[, gamma[, i]] * b[gamma[, i], i]
} else {
xb[, i] <- x[, gamma[, i]] %*% b[gamma[, i], i]
}
} else {
xb[, i] <- sapply(1:s, function(i) rep(1, n) * b[1, i])
}
}
} else {
if (sum(gamma) >= 1) {
xb <- x[, gamma] %*% b[gamma, ]
} else {
xb <- sapply(1:s, function(i) rep(1, n) * b[1, i])
}
}
corr_param <- 0.9
M <- matrix(corr_param, s, s)
diag(M) <- rep(1, s)
## wanna make it decomposable
Prime <- list(c(1:(s * .4), (s * .8):s),
c((s * .4):(s * .6)),
c((s * .65):(s * .75)),
c((s * .8):s))
G <- matrix(0, s, s)
for (i in 1:length(Prime)) {
G[Prime[[i]], Prime[[i]]] <- 1
}
# check
dimnames(G) <- list(1:s, 1:s)
length(gRbase::mcsMAT(G - diag(s))) > 0
var <- solve(BDgraph::rgwish(n = 1, adj = G, b = 3, D = M))
# change seeds to add randomness on error
set.seed(seed + 8493)
sd_err <- 0.5
if (is.infinite(t.df)) {
err <- matrix(rnorm(n * s, 0, sd_err), n, s) %*% chol(as.matrix(var))
} else {
err <- matrix(rt(n * s, t.df), n, s) %*% chol(as.matrix(var))
}
if (t0 == 0) {
b.re <- NA
z <- NA
y <- xb + err
if (random.intercept != 0) {
y <- y + matrix(rnorm(n * s, 0, sqrt(random.intercept)), n, s)
}
z <- sample(1:4, n, replace = T, prob = rep(1 / 4, 4))
return(list(y = y, x = x, b = b, gamma = gamma, z = model.matrix(~ factor(z) + 0)[, ],
b.re = b.re, Gy = G, mrfG = combnAll))
} else {
# add random effects
z <- t(rmultinom(n, size = 1, prob = c(.1, .2, .3, .4)))
z <- sample(1:t0, n, replace = T, prob = rep(1 / t0, t0))
set.seed(1683)
b.re <- rnorm(t0, 0, 2)
y <- matrix(b.re[z], nrow = n, ncol = s) + xb + err
return(list(
y = y, x = x, b = b, gamma = gamma, z = model.matrix(~ factor(z) + 0)[, ],
b.re = b.re, Gy = G, mrfG = combnAll
))
}
}To simulate data with sample size \(n=250\), responsible variables \(s=20\) and covariates \(p=300\), we can specify the corresponding
parameters in the function sim.ssur() as follows.
library("BayesSUR")
library("Matrix")
n <- 250
s <- 20
p <- 300
sim1 <- sim.ssur(n, s, p, seed = 1)To simulate data from \(4\)
individual groups with group indicator variables following the defaul
multinomial distribution \(multinomial(0.1,0.2,0.3,0.4)\), we can
simply add the argument t0 = 4 in the function
sim.ssur() as follows.
t0 <- 4
sim2 <- sim.ssur(n, s, p, t0, seed = 1) # learning data
sim2.val <- sim.ssur(n, s, p, t0, seed=101) # validation dataAccording to the guideline of prior specification in Zhao et al. 2023, we
first set the following parameters hyperpar and then
running the BayesSUR model with random effects via
betaPrior = "reGroup" (default
betaPrior = "independent" with spike-and-slab priors for
all coefficients). For illustration, we run a short
MCMC with nIter = 300 and
burnin = 100. Note that here the graph used for the Markov
random field prior is the true graph from the returned object of the
simulation sim2$mrfG.
hyperpar <- list(mrf_d = -2, mrf_e = 1.6, a_w0 = 100, b_w0 = 500, a_w = 15, b_w = 60)
set.seed(1038)
fit2 <- BayesSUR(
data = cbind(sim2$y, sim2$z, sim2$x),
Y = 1:s,
X_0 = s + 1:t0,
X = s + t0 + 1:p,
outFilePath = "sim2_mrf_re",
hyperpar = hyperpar,
gammaInit = "0",
betaPrior = "reGroup",
nIter = 300, burnin = 100,
covariancePrior = "HIW",
standardize = F,
standardize.response = F,
gammaPrior = "MRF",
mrfG = sim2$mrfG,
output_CPO = T
)## BayesSUR -- Bayesian Seemingly Unrelated Regression Modelling
## Reading input files ... ... successfull!
## Clearing and initialising output files
## Initialising the (SUR) MCMC Chain ... ... DONE!
## Drafting the output files with the start of the chain ... DONE!
##
## Starting 2 (parallel) chain(s) for 300 iterations:
## Temperature ladder updated, new temperature ratio : 1.1
## MCMC ends. --- Saving results and exiting
## Saved to : sim2_mrf_re/data_SSUR_****_out.txt
## Final w0 : 4.9971
## Final w : 2.29497
## Final tau : 0.293487 w/ proposal variance: 1.2229
## Final eta : 0.0471505
## -- Average Omega : 0
## Final temperature ratio : 1.1
##
## DONE, exiting!Check some summarized information of the results:
summary(fit2)## Call:
## BayesSUR(data = cbind(sim2$y, sim2$z, sim2$x), ...)
##
## CPOs:
## Min. 1st Qu. Median 3rd Qu. Max.
## 0.0001896996 0.0242732651 0.0348570615 0.0465600279 0.1312571329
##
## Number of selected predictors (mPIP > 0.5): 19 of 20x300
##
## Top 10 predictors on average mPIP across all responses:
## X.74 X.69 X.77 X.82 X.114 X.116 X.122 X.157 X.265
## 0.081840 0.049500 0.049500 0.049500 0.049500 0.049500 0.049500 0.049500 0.049500
## X.16
## 0.047015
##
## Top 10 responses on average mPIP across all predictors:
## X.8 X.10 X.5 X.19 X.11 X.9 X.6
## 0.012703000 0.010049000 0.007943333 0.006600000 0.005522333 0.004029667 0.003001667
## X.12 X.2 X.4
## 0.002852333 0.002769667 0.002404667
##
## Expected log pointwise predictive density (elpd) estimates:
## elpd.LOO = -16803.49, elpd.WAIC = -16799.94
##
## MCMC specification:
## iterations = 300, burn-in = 100, chains = 2
## gamma local move sampler: bandit
## gamma initialisation: 0
##
## Model specification:
## covariance prior: HIW
## gamma prior: MRF
##
## Hyper-parameters:
## a_w b_w nu a_tau b_tau a_eta b_eta mrf_d mrf_e a_w0 b_w0
## 15.0 60.0 22.0 0.1 10.0 0.1 1.0 -2.0 1.6 100.0 500.0Show the estimates of regression coefficients, variable selection indicators and residual graph
# show estimates
plot(fit2, estimator=c("beta","gamma","Gy"), type="heatmap", name.predictors = "auto")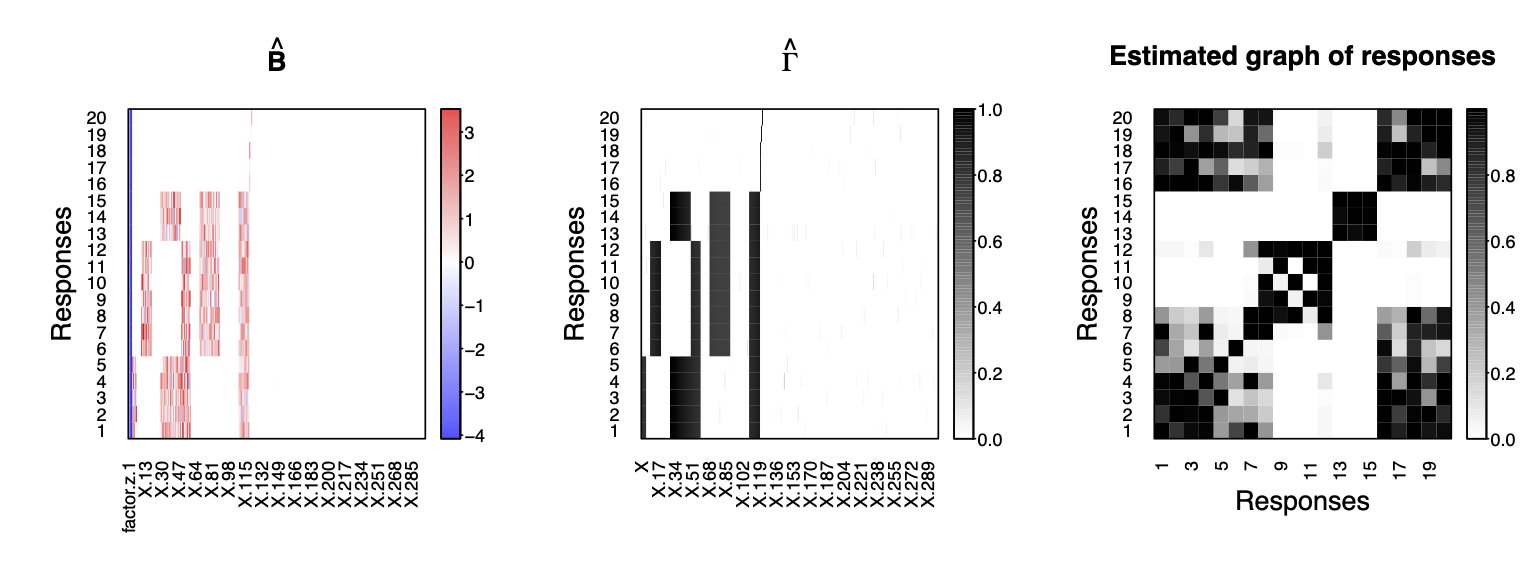
Compute the model performace with respect to variable selection
# compute accuracy, sensitivity, specificity of variable selection
gamma <- getEstimator(fit2)
(accuracy <- sum(data.matrix(gamma > 0.5) == sim2$gamma) / prod(dim(gamma)))## [1] 0.8725(sensitivity <- sum((data.matrix(gamma > 0.5) == 1) & (sim2$gamma == 1)) / sum(sim2$gamma == 1))## [1] 0.01558442(specificity <- sum((data.matrix(gamma > 0.5) == 0) & (sim2$gamma == 0)) / sum(sim2$gamma == 0))## [1] 0.9986616Compute the model performance with respect to response prediction
# compute RMSE and RMSPE for prediction performance
beta <- getEstimator(fit2, estimator = "beta", Pmax = .5, beta.type = "conditional")
(RMSE <- sqrt(sum((sim2$y - cbind(sim2$z, sim2$x) %*% beta)^2) / prod(dim(sim2$y))))## [1] 8.723454(RMSPE <- sqrt(sum((sim2.val$y - cbind(sim2.val$z, sim2.val$x) %*% beta)^2) / prod(dim(sim2.val$y))))## [1] 8.859939Compute the model performance with respect to coefficient bias
# compute bias of beta estimates
b <- sim2$b
b[sim2$gamma == 0] <- 0
(beta.l2 <- sqrt(sum((beta[-c(1:4), ] - b)^2) / prod(dim(b))))## [1] 0.5039502Compute the model performance with respect to covariance selection
g.re <- getEstimator(fit2, estimator = "Gy")
(g.accuracy <- sum((g.re > 0.5) == sim2$Gy) / prod(dim(g.re)))## [1] 0.585(g.sensitivity <- sum(((g.re > 0.5) == sim2$Gy)[sim2$Gy == 1]) / sum(sim2$Gy == 1))## [1] 0.2475248(g.specificity <- sum(((g.re > 0.5) == sim2$Gy)[sim2$Gy == 0]) / sum(sim2$Gy == 0))## [1] 0.9292929Leonardo Bottolo, Marco Banterle, Sylvia Richardson, Mika Ala-Korpela, Marjo-Riitta Järvelin, Alex Lewin (2021). A computationally efficient Bayesian seemingly unrelated regressions model for high-dimensional quantitative trait loci discovery. Journal of the Royal Statistical Society: Series C (Applied Statistics), 70(4):886-908. DOI: 10.1111/rssc.12490.
Zhi Zhao, Marco Banterle, Leonardo Bottolo, Sylvia Richardson, Alex Lewin, Manuela Zucknick (2021). BayesSUR: An R package for high-dimensional multivariate Bayesian variable and covariance selection in linear regression. Journal of Statistical Software, 100(11):1-32. DOI: 10.18637/jss.v100.i11.
Zhi Zhao, Marco Banterle, Alex Lewin, Manuela Zucknick (2023). Multivariate Bayesian structured variable selection for pharmacogenomic studies. Journal of the Royal Statistical Society: Series C (Applied Statistics), 73(2):420-443 qlad102. DOI: 10.1093/jrsssc/qlad102.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.