

The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
This is a R/Rcpp package BayesSurvive for Bayesian survival models with graph-structured selection priors for sparse identification of high-dimensional features predictive of survival (Hermansen et al., 2025; Madjar et al., 2021) (see the three models of the first column in the table below) and its extensions with the use of a fixed graph via a Markov Random Field (MRF) prior for capturing known structure of high-dimensional features (see the three models of the second column in the table below), e.g. disease-specific pathways from the Kyoto Encyclopedia of Genes and Genomes (KEGG) database.
| Model | Infer MRF_G |
Fix MRF_G |
|---|---|---|
Pooled |
✔ | ✔ |
CoxBVSSL |
✔ | ✔ |
Sub-struct |
✔ | ✔ |
Install the latest released version from CRAN
install.packages("BayesSurvive")Install the latest development version from GitHub
#install.packages("remotes")
remotes::install_github("ocbe-uio/BayesSurvive")library("BayesSurvive")
# Load the example dataset
data("simData", package = "BayesSurvive")
dataset = list("X" = simData[[1]]$X,
"t" = simData[[1]]$time,
"di" = simData[[1]]$status)## Initial value: null model without covariates
initial = list("gamma.ini" = rep(0, ncol(dataset$X)))
# Prior parameters
hyperparPooled = list(
"c0" = 2, # prior of baseline hazard
"tau" = 0.0375, # sd (spike) for coefficient prior
"cb" = 20, # sd (slab) for coefficient prior
"pi.ga" = 0.02, # prior variable selection probability for standard Cox models
"a" = -4, # hyperparameter in MRF prior
"b" = 0.1, # hyperparameter in MRF prior
"G" = simData$G # hyperparameter in MRF prior
)
## run Bayesian Cox with graph-structured priors
set.seed(123)
fit <- BayesSurvive(survObj = dataset, model.type = "Pooled", MRF.G = TRUE,
hyperpar = hyperparPooled, initial = initial,
nIter = 200, burnin = 100)
## show posterior mean of coefficients and 95% credible intervals
library("GGally")
plot(fit) +
coord_flip() +
theme(axis.text.x = element_text(angle = 90, size = 7))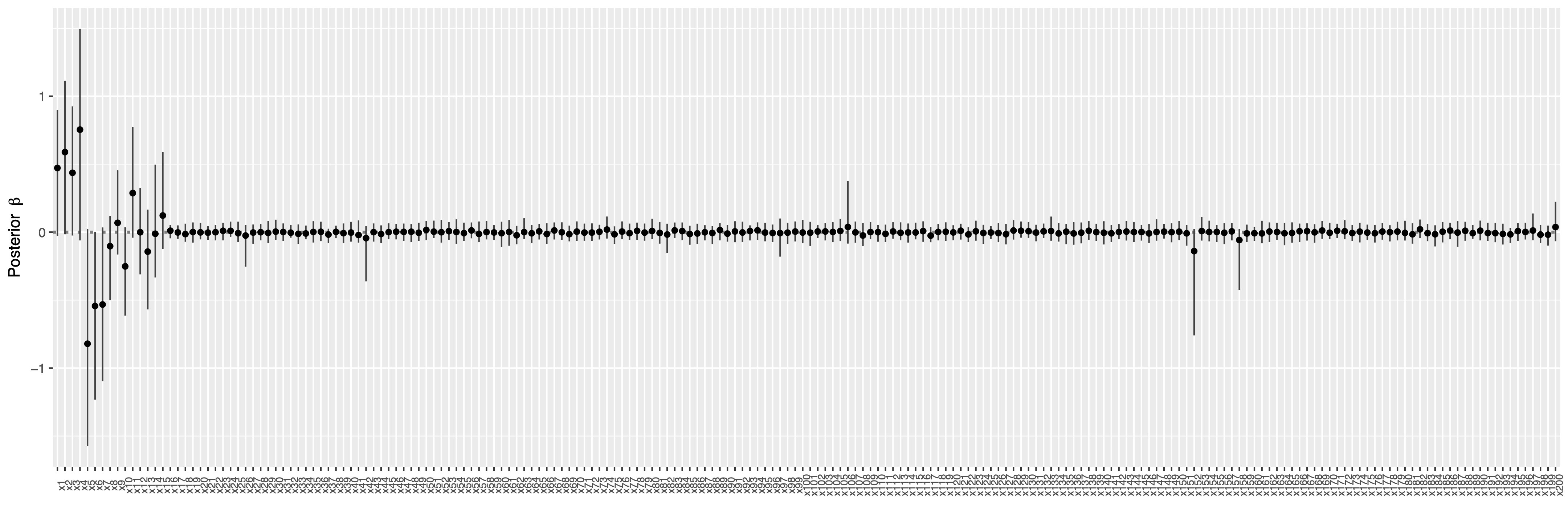
Show the index of selected variables by controlling Bayesian false discovery rate (FDR) at the level \(\alpha = 0.05\)
which( VS(fit, method = "FDR", threshold = 0.05) )#[1] 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 128The function BayesSurvive::plotBrier() can show the
time-dependent Brier scores based on posterior mean of coefficients or
Bayesian model averaging.
plotBrier(fit, survObj.new = dataset)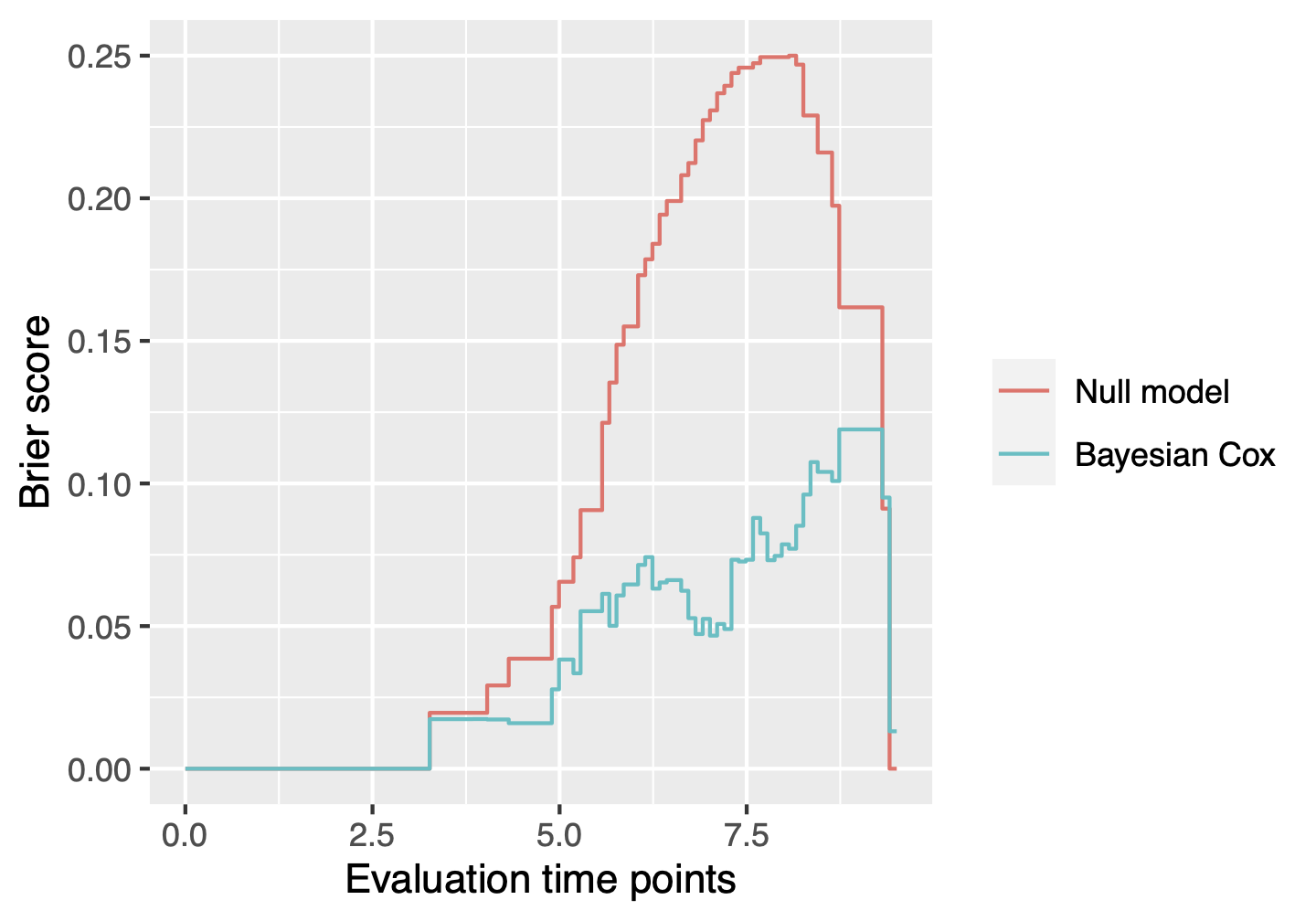
We can also use the function BayesSurvive::predict() to
obtain the Brier score at time 8.5, the integrated Brier score (IBS)
from time 0 to 8.5 and the index of prediction accuracy (IPA).
predict(fit, survObj.new = dataset, times = 8.5)## Brier(t=8.5) IBS(t:0~8.5) IPA(t=8.5)
## Null.model 0.2290318 0.08185316 0.0000000
## Bayesian.Cox 0.1037802 0.03020026 0.5468741The function BayesSurvive::predict() can estimate the
survival probabilities and cumulative hazards.
predict(fit, survObj.new = dataset, type = c("cumhazard", "survival"))# observation times cumhazard survival
## <int> <num> <num> <num>
## 1: 1 3.3 1.04e-04 1.00e+00
## 2: 2 3.3 3.88e-01 6.78e-01
## 3: 3 3.3 1.90e-06 1.00e+00
## 4: 4 3.3 1.94e-03 9.98e-01
## 5: 5 3.3 4.08e-04 1.00e+00
## ---
## 9996: 96 9.5 1.40e+01 8.21e-07
## 9997: 97 9.5 8.25e+01 1.45e-36
## 9998: 98 9.5 5.37e-01 5.85e-01
## 9999: 99 9.5 2.00e+00 1.35e-01
## 10000: 100 9.5 3.58e+00 2.79e-02hyperparPooled <- append(hyperparPooled, list("lambda" = 3, "nu0" = 0.05, "nu1" = 5))
fit2 <- BayesSurvive(survObj = list(dataset), model.type = "Pooled", MRF.G = FALSE,
hyperpar = hyperparPooled, initial = initial, nIter = 10)# specify a fixed joint graph between two subgroups
hyperparPooled$G <- Matrix::bdiag(simData$G, simData$G)
dataset2 <- simData[1:2]
dataset2 <- lapply(dataset2, setNames, c("X", "t", "di", "X.unsc", "trueB"))
fit3 <- BayesSurvive(survObj = dataset2,
hyperpar = hyperparPooled, initial = initial,
model.type="CoxBVSSL", MRF.G = TRUE,
nIter = 10, burnin = 5)fit4 <- BayesSurvive(survObj = dataset2,
hyperpar = hyperparPooled, initial = initial,
model.type="CoxBVSSL", MRF.G = FALSE,
nIter = 3, burnin = 0)Tobias Østmo Hermansen, Manuela Zucknick, Zhi Zhao (2025). Bayesian Cox model with graph-structured variable selection priors for multi-omics biomarker identification. arXiv. DOI: arXiv.2503.13078.
Katrin Madjar, Manuela Zucknick, Katja Ickstadt, Jörg Rahnenführer (2021). Combining heterogeneous subgroups with graph‐structured variable selection priors for Cox regression. BMC Bioinformatics, 22(1):586. DOI: 10.1186/s12859-021-04483-z.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.