The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
author: Jacek Białek, University of Lodz, Statistics Poland
Goals of PriceIndices are as follows: a) data processing before price index calculations; b) bilateral and multilateral price index calculations; c) extending multilateral price indices. You can download the package documentation from here. Too read more about the package please see (and cite :)) papers:
Białek, J. (2021). PriceIndices – a New R Package for Bilateral and Multilateral Price Index Calculations, Statistika – Statistics and Economy Journal, Vol. 2/2021, 122-141, Czech Statistical Office, Praga.
Białek, J. (2022). Scanner data processing in a newest version of the PriceIndices package, Statistical Journal of the IAOS, 38 (4), 1369-1397, DOI: 10.3233/SJI-220963.
Białek, J. (2023). Scanner data processing and price index calculations in the PriceIndices R package, Slovak Statistics and Demography, 3, 7-20, ISNN: 1210-1095.
You can install the released version of PriceIndices from CRAN with:
install.packages("PriceIndices")You can install the development version of PriceIndices from GitHub with:
library("remotes")
remotes::install_github("JacekBialek/PriceIndices")This package includes 10 data sets: artificial and real.
1) dataAGGR
The first one, dataAGGR, can be used to demonstrate the data_aggregating function. This is a collection of artificial scanner data on milk products sold in three different months and it contains the following columns: time - dates of transactions (Year-Month-Day: 4 different dates); prices - prices of sold products (PLN); quantities - quantities of sold products (liters); prodID - unique product codes (3 different prodIDs); retID - unique codes identifying outlets/retailer sale points (4 different retIDs); description - descriptions of sold products (two subgroups: goat milk, powdered milk).
2) dataMATCH
The second one, dataMATCH, can be used to demonstrate the data_matching function and it will be described in the next part of the guidelines. Generally, this artificial data set contains the following columns: time - dates of transactions (Year-Month-Day); prices - prices of sold products; quantities - quantities of sold products; codeIN - internal product codes from the retailer; codeOUT - external product codes, e.g. GTIN or SKU in the real case; description - descriptions of sold products, eg. ‘product A’, ‘product B’, etc.
3) dataCOICOP
The third one, dataCOICOP, is a ollection of real scanner data on the sale of milk products sold in a period: Dec, 2020 - Feb, 2022. It is a data frame with 10 columns and 139600 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day); prices - prices of sold products (PLN); quantities - quantities of sold products; description - descriptions of sold products (original: in Polish); codeID - retailer product codes; retID - IDs of retailer outlets; grammage - product grammages; unit - sales units, e.g. ‘kg’, ‘ml’, etc.; category - product categories (in English) corresponding to COICOP 6 levels; coicop6 - identifiers of local COICOP 6 groups (6 levels). Please note that this data set can serve as a training or testing set in product classification using machine learning methods.
4) data_DOWN_UP_SIZED
This data set, data_DOWN_UP_SIZED, is a collection of scanner data on the sale of coffee in the period from January 2024 to February 2024 and it contains downsized products (see the shrinkflation function). It is a data frame with 6 columns and 51 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day), prices - prices of sold products [PLN], quantities - quantities of sold products (in units resulting the product description), codeIN - unique internal product codes (retaler product codes), codeOUT - unique external product codes (e.g. GTIN, EAN, SKU), description - descriptions of sold coffee products.
5) milk
This data set, milk, is a collection of scaner data on the sale of milk in one of Polish supermarkets in the period from December 2018 to August 2020. It is a data frame with 6 columns and 4386 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day); prices - prices of sold products (PLN); quantities - quantities of sold products (liters); prodID - unique product codes obtained after product matching (data set contains 68 different prodIDs); retID - unique codes identifying outlets/retailer sale points (data set contains 5 different retIDs); description - descriptions of sold milk products (data set contains 6 different product descriptions corresponding to subgroups of the milk group).
6) coffee
This data set, coffee, is a collection of scanner data on the sale of coffee in one of Polish supermarkets in the period from December 2017 to October 2020. It is a data frame with 6 columns and 42561 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day); prices - prices of sold products (PLN); quantities - quantities of sold products (kg); prodID - unique product codes obtained after product matching (data set contains 79 different prodIDs); retID - unique codes identifying outlets/retailer sale points (data set contains 20 different retIDs); description - descriptions of sold coffee products (data set contains 3 different product descriptions corresponding to subgroups of the coffee group).
7) sugar
This data set, sugar, is a collection of scanner data on the sale of coffee in one of Polish supermarkets in the period from December 2017 to October 2020. It is a data frame with 6 columns and 7666 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day); prices - prices of sold products (PLN); quantities - quantities of sold products (kg); prodID - unique product codes obtained after product matching (data set contains 11 different prodIDs); retID - unique codes identifying outlets/retailer sale points (data set contains 20 different retIDs); description - descriptions of sold sugar products (data set contains 3 different product descriptions corresponding to subgroups of the sugar group).
8) dataU
This data set, dataU, is a collection of artificial scanner data on 6 products sold in Dec, 2018. Product descriptions contain the information about their grammage and unit. It is a data frame with 5 columns and 6 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day); prices - prices of sold products (PLN); quantities - quantities of sold products (item); prodID - unique product codes; description - descriptions of sold products (data set contains 6 different product descriptions).
9) dataMARS
This data set, dataMARS, is a collection of artificial scanner data on shirts for testing the MARS method. It contains 9 columns and 44 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day), prices - prices of sold products [PLN], quantities - quantities of sold products, prodID - unique product identifiers (data set contains 28 different prodIDs), description - descriptions (labels) of sold shirts (data set contains 12 different descriptions), brand - brand of sold shirts (data set contains 2 different brands: X and Y), gender - gender of the person for whom the shirt is dedicated (M or F), size - size of shirts (M, L, and XL), fabric - fabric of shirts (cotton, polyester, blend).
10) dataRSM This data set, dataRSM, is a collection of scanner data on the sale of rice, sugar and milk products in one of Polish supermarkets in the period from December 2023 to January 2025. It contains 9 columns and 8090 rows. The used variables are as follows: time - dates of transactions (Year-Month-Day), prices - prices of sold products [PLN], quantities - quantities of sold products, retID - unique codes identifying outlets/retailer sale points (data set contains 4 different retIDs), description - descriptions (labels) of sold products (data set contains 152 different descriptions), retailer_code - retailer codes for product definition (134 retailer codes), EAN_code - EAN codes (bar codes) for product definition (138 EAN codes), category - product categories at the 6-digit COICOP level (4 categories), and subcategory - product subcategories from 7-digit COICOP level (11 subcategories). Please note that the data frame does not contain the prodID column, so it must be defined (or specified) before calculating price indices.
The set milk represents a typical data frame used in the package for most calculations and is organized as follows:
library(PriceIndices)
head(milk)
#> time prices quantities prodID retID description
#> 1 2018-12-01 8.78 9.0 14215 2210 powdered milk
#> 2 2019-01-01 8.78 13.5 14215 2210 powdered milk
#> 3 2019-02-01 8.78 0.5 14215 1311 powdered milk
#> 4 2019-02-01 8.78 8.0 14215 2210 powdered milk
#> 5 2019-03-01 8.78 0.5 14215 1311 powdered milk
#> 6 2019-03-01 8.78 1.5 14215 2210 powdered milkAvailable subgroups of sold milk are
unique(milk$description)
#> [1] "powdered milk" "low-fat milk pasteurized"
#> [3] "low-fat milk UHT" "full-fat milk pasteurized"
#> [5] "full-fat milk UHT" "goat milk"Generating artificial scanner data sets in the package
The package includes the generate function which provides an artificial scanner data sets where prices and quantities are lognormally distributed. The characteristics for these lognormal distributions are set by pmi, sigma, qmi and qsigma parameters. This function works for the fixed number of products and outlets (see n and r parameters). The generated data set is ready for further price index calculations. For instance:
dataset<-generate(pmi=c(1.02,1.03,1.04),psigma=c(0.05,0.09,0.02),
qmi=c(3,4,4),qsigma=c(0.1,0.1,0.15),
start="2020-01")
head(dataset)
#> time prices quantities prodID retID
#> 1 2020-01-01 2.67 19 1 1
#> 2 2020-01-01 2.67 20 2 1
#> 3 2020-01-01 2.89 21 3 1
#> 4 2020-01-01 2.72 19 4 1
#> 5 2020-01-01 2.93 19 5 1
#> 6 2020-01-01 2.66 21 6 1From the other hand you can use tindex function to obtain the theoretical value of the unweighted price index for lognormally distributed prices (the month defined by start parameter plays a role of the fixed base period). The characteristics for these lognormal distributions are set by pmi and sigma parameters. The ratio parameter is a logical parameter indicating how we define the theoretical unweighted price index. If it is set to TRUE then the resulting value is a ratio of expected price values from compared months; otherwise the resulting value is the expected value of the ratio of prices from compared months.The function provides a data frame consisting of dates and corresponding expected values of the theoretical unweighted price index. For example:
tindex(pmi=c(1.02,1.03,1.04),psigma=c(0.05,0.09,0.02),start="2020-01",ratio=FALSE)
#> date tindex
#> 1 2020-01 1.000000
#> 2 2020-02 1.012882
#> 3 2020-03 1.019131The User may also generate an artificial scanner dataset where prices are lognormally distributed and quantities are calculated under the assumption that consumers have CES (Constant Elasticity of Substitution) preferences and their spending on all products is fixed (see the generate_CES function). Please watch the following example:
#Generating an artificial dataset (the elasticity of substitution is 1.25)
df<-generate_CES(pmi=c(1.02,1.03),psigma=c(0.04,0.03),
elasticity=1.25,start="2020-01",n=100,days=TRUE)
head(df)
#> time prices quantities prodID retID
#> 1 2020-01-03 2.66 4.412698 1 1
#> 2 2020-01-02 2.53 2.340218 2 1
#> 3 2020-01-23 2.93 3.732539 3 1
#> 4 2020-01-01 2.67 4.239343 4 1
#> 5 2020-01-11 2.96 7.229107 5 1
#> 6 2020-01-20 2.71 8.003085 6 1Now, we can verify the value of elasticity of substitution using this generated dataset:
#Verifying the elasticity of substitution
elasticity(df, start="2020-01",end="2020-02")
#> [1] 1.25data_preparing
This function returns a prepared data frame based on the user’s data set (you can check if your data set it is suitable for further price index calculation by using data_check function). The resulting data frame is ready for further data processing (such as data selecting, matching or filtering) and it is also ready for price index calculations (if only it contains the required columns). The resulting data frame is free from missing values, negative and (optionally) zero prices and quantities. As a result, the column time is set to be Date type (in format: ‘Year-Month-01’), while the columns prices and quantities are set to be numeric. If the description parameter is set to TRUE then the column description is set to be character type (otherwise it is deleted). Please note that the milk set is an already prepared dataset but let us assume for a moment that we want to make sure that it does not contain missing values and we do not need the column description for further calculations. For this purpose, we use the data_preparing function as follows:
head(data_preparing(milk, time="time",prices="prices",quantities="quantities"))
#> time prices quantities
#> 1 2018-12-01 8.78 9.0
#> 2 2019-01-01 8.78 13.5
#> 3 2019-02-01 8.78 0.5
#> 4 2019-02-01 8.78 8.0
#> 5 2019-03-01 8.78 0.5
#> 6 2019-03-01 8.78 1.5data_imputing
This function imputes missing prices (unit values) and (optionally) zero prices by using one of the following methods: carry forward/backward, overall mean, class mean (targeted mean). The imputation can be done for each outlet separately or for aggregated data (see the outlets parameter). For the carry forward/backward method: if a missing product has a previous price then that previous price is carried forward until the next real observation. If there is no previous price then the next real observation is found and carried backward. For the overall mean method: the procedure is similar, except that the imputed price is based on the previously recorded price multiplied (or divided - in the case of the next recorded price) by the price index determined for the quoted and imputed period. The user can select the index formula via the formula parameter. For the class mean method (also known as targeted mean method): the procedure is analogous to the overall mean method, but the price index is determined for the product class specified by the class parameter. The quantities for imputed prices are set to zero. The function returns a data frame (monthly aggregated) which is ready for price index calculations.
#Creating a data frame with zero prices (df)
data<-dplyr::filter(milk,time>=as.Date("2018-12-01") & time<=as.Date("2019-03-01"))
sample<-dplyr::sample_n(data, 100)
rest<-setdiff(data, sample)
sample$prices<-0
df<-rbind(sample, rest)
#The Fisher price index calculated for the original data set
fisher(df, "2018-12","2019-03")
#> [1] 0.9694849
#Zero price imputations:
df2<-data_imputing(df, start="2018-12", end="2019-03",
zero_prices=TRUE,
outlets=TRUE)
#The Fisher price index calculated for the data set with imputed prices:
fisher(df2, "2018-12","2019-03")
#> [1] 0.9694771data_aggregating
The function aggregates the user’s data frame over time and/or over outlets. Consequently, we obtain monthly data, where the unit value is calculated instead of a price for each prodID observed in each month (the time column gets the Date format: “Year-Month-01”). If paramter join_outlets is TRUE, then the function also performs aggregation over outlets (retIDs) and the retID column is removed from the data frame. The main advantage of using this function is the ability to reduce the size of the data frame and the time needed to calculate the price index. For instance, let us consider the following data set:
dataAGGR
#> time prices quantities prodID retID description
#> 1 2018-12-01 10 100 400032 4313 goat milk
#> 2 2018-12-01 15 100 400032 1311 goat milk
#> 3 2018-12-01 20 100 400032 1311 goat milk
#> 4 2020-07-01 20 100 400050 1311 goat milk
#> 5 2020-08-01 30 50 400050 1311 goat milk
#> 6 2020-08-01 40 50 400050 2210 goat milk
#> 7 2018-12-01 15 200 403249 2210 powdered milk
#> 8 2018-12-01 15 200 403249 2210 powdered milk
#> 9 2018-12-01 15 300 403249 2210 powdered milkAfter aggregating this data set over time and outlets we obtain:
data_aggregating(dataAGGR)
#> # A tibble: 4 × 4
#> time prodID prices quantities
#> <date> <int> <dbl> <int>
#> 1 2018-12-01 400032 15 300
#> 2 2018-12-01 403249 15 700
#> 3 2020-07-01 400050 20 100
#> 4 2020-08-01 400050 35 100data_unit
The function returns the user’s data frame with two additional columns: grammage and unit (both are character type). The values of these columns are extracted from product descriptions on the basis of provided units. Please note, that the function takes into consideration a sign of the multiplication, e.g. if the product description contains: ‘2x50 g’, we will obtain: grammage: 100 and unit: g for that product (for multiplication set to ‘x’). For example:
data_unit(dataU,units=c("g|ml|kg|l"),multiplication="x")
#> time prices quantities prodID description grammage unit
#> 1 2018-12-01 8.00 200 40033 drink 0,75l 3% corma 0.75 l
#> 2 2018-12-01 5.20 300 12333 sugar 0.5kg 0.50 kg
#> 3 2018-12-01 10.34 100 20345 milk 4x500ml 2000.00 ml
#> 4 2018-12-01 2.60 500 15700 xyz 3 4.34 xyz 200 g 200.00 g
#> 5 2018-12-01 12.00 1000 13022 abc 1.00 item
#> 6 2019-01-01 3.87 250 10011 ABC 2A/45 350 g mnk 350.00 gdata_norm
The function returns the user’s data frame with two transformed columns: grammage and unit, and two rescaled columns: prices and quantities. The above-mentioned transformation and rescaling take into consideration the user rules. Recalculated prices and quantities concern grammage units defined as the second parameter in the given rule. For instance:
# Preparing a data set
data<-data_unit(dataU,units=c("g|ml|kg|l"),multiplication="x")
# Normalization of grammage units
data_norm(data, rules=list(c("ml","l",1000),c("g","kg",1000)))
#> time prices quantities prodID description grammage unit
#> 1 2018-12-01 5.17000 200.0 20345 milk 4x500ml 2.00 l
#> 2 2018-12-01 10.66667 150.0 40033 drink 0,75l 3% corma 0.75 l
#> 3 2018-12-01 13.00000 100.0 15700 xyz 3 4.34 xyz 200 g 0.20 kg
#> 4 2019-01-01 11.05714 87.5 10011 ABC 2A/45 350 g mnk 0.35 kg
#> 5 2018-12-01 10.40000 150.0 12333 sugar 0.5kg 0.50 kg
#> 6 2018-12-01 12.00000 1000.0 13022 abc 1.00 itemdata_selecting
The function returns a subset of the user’s data set obtained by selection based on keywords and phrases defined by parameters: include, must and exclude (an additional column coicop is optional). Providing values of these parameters, please remember that the procedure distinguishes between uppercase and lowercase letters only when sensitivity is set to TRUE.
For instance, please use
subgroup1<-data_selecting(milk, include=c("milk"), must=c("UHT"))
head(subgroup1)
#> time prices quantities prodID retID description
#> 1 2018-12-01 2.97 78 17034 1311 low-fat milk uht
#> 2 2018-12-01 2.97 167 17034 2210 low-fat milk uht
#> 3 2018-12-01 2.97 119 17034 6610 low-fat milk uht
#> 4 2018-12-01 2.97 32 17034 7611 low-fat milk uht
#> 5 2018-12-01 2.97 54 17034 8910 low-fat milk uht
#> 6 2019-01-01 2.95 71 17034 1311 low-fat milk uhtto obtain the subset of milk limited to UHT category:
unique(subgroup1$description)
#> [1] "low-fat milk uht" "full-fat milk uht"You can use
subgroup2<-data_selecting(milk, must=c("milk"), exclude=c("past","goat"))
head(subgroup2)
#> time prices quantities prodID retID description
#> 1 2018-12-01 8.78 9.0 14215 2210 powdered milk
#> 2 2019-01-01 8.78 13.5 14215 2210 powdered milk
#> 3 2019-02-01 8.78 0.5 14215 1311 powdered milk
#> 4 2019-02-01 8.78 8.0 14215 2210 powdered milk
#> 5 2019-03-01 8.78 0.5 14215 1311 powdered milk
#> 6 2019-03-01 8.78 1.5 14215 2210 powdered milkto obtain the subset of milk with products which are not pasteurized and which are not goat:
unique(subgroup2$description)
#> [1] "powdered milk" "low-fat milk uht" "full-fat milk uht"data_matching
If you have a dataset with information about products sold but they are not matched you can use the data_matching function. In an optimal situation, your data frame contains the codeIN, codeOUT and description columns (see documentation), which in practice will contain retailer codes, GTIN or SKU codes and product labels, respectively. The data_matching function returns a data set defined in the first parameter (data) with an additional column (prodID). Two products are treated as being matched if they have the same prodID value. The procedure of generating the above-mentioned additional column depends on the set of chosen columns for matching (see documentation for details). For instance, let us suppose you want to obtain matched products from the following, artificial data set:
head(dataMATCH)
#> time prices quantities codeIN codeOUT retID description
#> 1 2018-12-01 9.416371 309 1 1 1 product A
#> 2 2019-01-01 9.881875 325 1 5 1 product A
#> 3 2019-02-01 12.611826 327 1 1 1 product A
#> 4 2018-12-01 9.598252 309 3 2 1 product A
#> 5 2019-01-01 9.684900 325 3 2 1 product A
#> 6 2019-02-01 9.358420 327 3 2 1 product ALet us assume that products with two identical codes (codeIN and codeOUT) or one of the codes identical and an identical description are automatically matched. Products are also matched if they have one of the codes identical and the Jaro-Winkler similarity of their descriptions is bigger than the fixed precision value (see documentation - Case 1). Let us also suppose that you want to match all products sold in the interval: December 2018 - February 2019. If you use the data_matching function (as below), an additional column (prodID) will be added to your data frame:
data1<-data_matching(dataMATCH, start="2018-12",end="2019-02", codeIN=TRUE, codeOUT=TRUE, precision=.98, interval=TRUE)
head(data1)
#> time prices quantities codeIN codeOUT retID description prodID
#> 1 2018-12-01 9.416371 309 1 1 1 product A 4
#> 2 2019-01-01 9.881875 325 1 5 1 product A 4
#> 3 2019-02-01 12.611826 327 1 1 1 product A 4
#> 4 2018-12-01 9.598252 309 3 2 1 product A 8
#> 5 2019-01-01 9.684900 325 3 2 1 product A 8
#> 6 2019-02-01 9.358420 327 3 2 1 product A 8Let us now suppose you do not want to consider codeIN while matching and that products with an identical description are to be matched too:
data2<-data_matching(dataMATCH, start="2018-12",end="2019-02",
codeIN=FALSE, onlydescription=TRUE, interval=TRUE)
head(data2)
#> time prices quantities codeIN codeOUT retID description prodID
#> 1 2018-12-01 9.416371 309 1 1 1 product A 7
#> 2 2019-01-01 9.881875 325 1 5 1 product A 7
#> 3 2019-02-01 12.611826 327 1 1 1 product A 7
#> 4 2018-12-01 9.598252 309 3 2 1 product A 7
#> 5 2019-01-01 9.684900 325 3 2 1 product A 7
#> 6 2019-02-01 9.358420 327 3 2 1 product A 7Now, having a prodID column, your datasets are ready for further price index calculations, e.g.:
fisher(data1, start="2018-12", end="2019-02")
#> [1] 1.018419
jevons(data2, start="2018-12", end="2019-02")
#> [1] 1.074934data_filtering
This function returns a filtered data set, i.e. a reduced user’s data frame with the same columns and rows limited by a criterion defined by the filters parameter (see documentation). If the set of filters is empty then the function returns the original data frame (defined by the data parameter). On the other hand, if all filters are chosen, i.e. filters=c(extremeprices, dumpprices, lowsales), then these filters work independently and a summary result is returned. Please note that both variants of the extremeprices filter can be chosen at the same time, i.e. plimits and pquantiles, and they work also independently. For example, let us assume we consider three filters: filter1 is to reject 1% of the lowest and 1% of the highest price changes comparing March 2019 to December 2018, filter2 is to reject products with the price ratio being less than 0.5 or bigger than 2 in the same time, filter3 rejects the same products as filter2 rejects and also products with relatively low sale in compared months, filter4 rejects products with the price ratio being less than 0.9 and with the expenditure ratio being less than 0.8 in the same time.
filter1<-data_filtering(milk,start="2018-12",end="2019-03",
filters=c("extremeprices"),pquantiles=c(0.01,0.99))
filter2<-data_filtering(milk,start="2018-12",end="2019-03",
filters=c("extremeprices"),plimits=c(0.5,2))
filter3<-data_filtering(milk,start="2018-12",end="2019-03",
filters=c("extremeprices","lowsales"),plimits=c(0.5,2))
filter4<-data_filtering(milk,start="2018-12",end="2019-03",
filters=c("dumpprices"),dplimits=c(0.9,0.8))These three filters differ from each other with regard to the data reduction level:
data_without_filters<-data_filtering(milk,start="2018-12",end="2019-03",filters=c())
nrow(data_without_filters)
#> [1] 413
nrow(filter1)
#> [1] 378
nrow(filter2)
#> [1] 381
nrow(filter3)
#> [1] 170
nrow(filter4)
#> [1] 374You can also use data_filtering for each pair of subsequent months from the considered time interval under the condition that this filtering is done for each outlet (retID) separately, e.g.
filter1B<-data_filtering(milk,start="2018-12",end="2019-03",
filters=c("extremeprices"),pquantiles=c(0.01,0.99),
interval=TRUE, outlets=TRUE)
nrow(filter1B)
#> [1] 773Two more useful functions are included for the procedure of scanner data. The first, data_reducing, returns a data set containing sufficiently numerous matched products in the indicated groups (see documentation). It reduces the dataset to only a representative set of products that have appeared in sufficient numbers in the sales offer:
sugar.<-dplyr::filter(sugar, time==as.Date("2018-12-01") | time==as.Date("2019-12-01"))
nrow(sugar.)
#> [1] 435
sugar_<-data_reducing(sugar., start="2018-12", end="2019-12",by="description", minN=5)
nrow(sugar_)
#> [1] 275The second function, shrinkflation, detects and summarises downsized and upsized products. The function detects phenomena such as: shrinkflation, shrinkdeflation, sharkflation,unshrinkdeflation, unshrinkflation, sharkdeflation (see the type parameter). It returns a list containing the following objects: df_changes - data frame with detailed information on downsized and upsized products with the whole history of size changes, df_type - data frame with recognized type of products, df_overview - a table with basic summary of all detected products grouped by the type parameter, products_detected with prodIDs of products indicated by the type parameter, df_detected being a subset of the data frame with only detected products, df_reduced which is the difference of the input data frame and the data frame containing the detected products, and df_summary which provides basic statistics for all detected downsized and upsized products (including their share in the total number of products and mean price and size changes). For instance:
#Data matching over time
df<-data_matching(data=data_DOWN_UP_SIZED, start="2024-01", end="2024-02",
codeIN=TRUE,codeOUT=TRUE,description=TRUE,
onlydescription=FALSE,precision=0.9,interval=FALSE)
# Extraction of information about grammage
df<-data_unit(df,units=c("g|ml|kg|l"),multiplication="x")
# Price standardization
df<-data_norm(df, rules=list(c("ml","l",1000),c("g","kg",1000)))
# Downsized and upsized products detection
result<-shrinkflation(data=df, start="2024-01","2024-02", prec=3, interval=FALSE, type="shrinkflation")
# result$df_changes
result$df_type
#> IDs size_change price_orig_change price_norm_change detected_type
#> 1 7 -20.000 -18.824 1.471 shrinkflation
#> 2 10 -15.000 -10.000 5.882 shrinkflation
#> 3 10 -19.048 -10.000 11.176 shrinkflation
#> 4 10 -14.286 -10.000 5.000 shrinkflation
#> 5 11 -2.500 1.040 3.632 sharkflation
#> 6 12 -4.000 -0.794 3.340 shrinkflation
#> 7 14 -10.000 -40.000 -33.333 shrinkdeflation
#> 8 16 -15.000 15.000 35.294 sharkflation
#> 9 18 20.000 5.000 -12.500 unshrinkdeflation
#> 10 20 25.000 5.557 -15.556 unshrinkdeflation
#> 11 22 12.500 37.777 22.469 unshrinkflation
#> 12 24 33.333 50.000 12.500 unshrinkflation
#> 13 26 5.000 -12.500 -16.666 sharkdeflation
#> descriptions
#> 1 coffee super 0,4 l ; coffee super 0,5 l , coffee super 0,4 l
#> 2 coffee ABC 200g ; coffee ABC 210g , coffee ABC 170g ; coffee ABC 180g
#> 3 coffee ABC 200g ; coffee ABC 210g , coffee ABC 170g ; coffee ABC 180g
#> 4 coffee ABC 200g ; coffee ABC 210g , coffee ABC 170g ; coffee ABC 180g
#> 5 coffee GHI 2 x 400g , coffee GHI 2 x 390g
#> 6 coffee JKL 250 ml , coffee JKL 240 ml ; coffee JKL 250 ml
#> 7 coffee F 200g , coffee F 180g
#> 8 coffee G 200g , coffee G 170g
#> 9 coffee H 200g , coffee H 240g
#> 10 coffee M 400g , coffee M 500g
#> 11 coffee K 400g , coffee K 450g
#> 12 coffee L 300g , coffee L 400g
#> 13 coffee LX 200g , coffee LX 210g
#> dates
#> 1 2024-01 , 2024-02
#> 2 2024-01 , 2024-02
#> 3 2024-01 , 2024-02
#> 4 2024-01 , 2024-02
#> 5 2024-01 , 2024-02
#> 6 2024-01 , 2024-02
#> 7 2024-01 , 2024-02
#> 8 2024-01 , 2024-02
#> 9 2024-01 , 2024-02
#> 10 2024-01 , 2024-02
#> 11 2024-01 , 2024-02
#> 12 2024-01 , 2024-02
#> 13 2024-01 , 2024-02
result$df_overview
#> # A tibble: 6 × 3
#> `type of phenomenon detected` number of detected prod…¹ shares [%] of detect…²
#> <chr> <int> <dbl>
#> 1 sharkdeflation 1 7.69
#> 2 sharkflation 2 15.4
#> 3 shrinkdeflation 1 7.69
#> 4 shrinkflation 3 23.1
#> 5 unshrinkdeflation 2 15.4
#> 6 unshrinkflation 2 15.4
#> # ℹ abbreviated names: ¹`number of detected products`,
#> # ²`shares [%] of detected products`
# result$products_detected
# result$df_detected
# result$df_reduced
result$df_summary
#> stats value
#> 1 Detected product shares: ---------------
#> 2 number of all products 13
#> 3 number of detected products 3
#> 4 share of detected products 23.077 %
#> 5 turnover of all products 289430
#> 6 turnover of detected products 73380
#> 7 turnover share of detected products 25.353 %
#> 8 Average measures: ---------------
#> 9 mean size change of detected products -14.467 %
#> 10 mean price change of detected products -9.923 %
#> 11 mean unit price change of detected products 5.374 %
#> 12 median size change of detected products -15 %
#> 13 median price change of detected products -10 %
#> 14 median unit price change of detected products 5 %
#> 15 Volatility measures: ---------------
#> 16 standard deviation of size change 6.354 %
#> 17 standard deviation of price change 6.375 %
#> 18 standard deviation of unit price change 3.655 %
#> 19 volatility coefficient of size change -0.439
#> 20 volatility coefficient of price change -0.642
#> 21 volatility coefficient of unit price change 0.68MARS
This function groups prodIDs into strata (‘products’) by balancing two measures: an explained variance (R squared) measure for the ‘homogeneity’ of prodIDs within products, while the second expresses the degree to which products can be ‘matched’ over time with respect to a comparison period. The resulting product ‘match adjusted R squared’ (MARS) combines explained variance in product prices with product match over time, so that different stratification schemes can be ranked according to the combined measure. Any combination of attributes is taken into account when creating stratas. For example, for a set of attributes A, B, C, the stratas created by the following attribute combinations are considered: A, B, C, A-B, A-C, B-C, A-B-C.The function returns a list with the following elements: scores (with scores for degrees of product match and product homogeneity, as well as for MARS measure), best_partition (with the name of the partition for which the highest indication of the MARS measure was obtained), and data_MARS (with a data frame obtained by replacing the original prodIDs with identifiers created based on the selected best partition). An example:
df<-MARS(data=dataMARS,
start="2025-05",
end="2025-09",
attributes=c("brand","size","fabric"),
strategy="two_months")
#Results:
df$scores
#> partition product_match product_homogeneity MARS
#> 1 brand 1.0000000 0.04223639 0.04223639
#> 2 size 1.0000000 0.14589023 0.14589023
#> 3 fabric 1.0000000 0.47340153 0.47340153
#> 4 brand-size 0.9494585 0.17168061 0.16300362
#> 5 brand-fabric 0.9494585 0.96526753 0.91648144
#> 6 size-fabric 1.0000000 0.96526753 0.96526753
#> 7 brand-size-fabric 0.9494585 0.96526753 0.91648144available
The function returns all values from the indicated column (defined by the type parameter) which occur at least once in one of compared periods or in a given time interval. Possible values of the type parameter are: retID, prodID, codeIN, codeOUT or description (see documentation). If the interval parameter is set to FALSE, then the function compares only periods defined by period1 and period2. Otherwise the whole time period between period1 and period2 is considered. For example:
available(milk, period1="2018-12", period2="2019-12", type="retID",interval=TRUE)
#> [1] 2210 1311 6610 7611 8910matched
The function returns all values from the indicated column (defined by the type parameter) which occur simultaneously in the compared periods or in a given time interval.Possible values of the type parameter are: retID, prodID, codeIN, codeOUT or description (see documentation). If the interval parameter is set to FALSE, then the function compares only periods defined by period1 and period2. Otherwise the whole time period between period1 and period2 is considered. For example:
matched(milk, period1="2018-12", period2="2019-12", type="prodID",interval=TRUE)
#> [1] 14216 15404 17034 34540 60010 70397 74431 82827 82830 82919
#> [11] 94256 400032 400033 400189 400194 400195 400196 401347 401350 402263
#> [21] 402264 402293 402569 402570 402601 402602 402609 403249 404004 404005
#> [31] 405419 405420 406223 406224 406245 406246 406247 407219 407220 407669
#> [41] 407670 407709 407859 407860 400099matched_index
The function returns a ratio of values from the indicated column that occur simultaneously in the compared periods or in a given time interval to all available values from the above-mentioned column (defined by the type parameter) at the same time. Possible values of the type parameter are: retID, prodID, codeIN, codeOUT or description (see documentation). If the interval parameter is set to FALSE, then the function compares only periods defined by period1 and period2. Otherwise the whole time period between period1 and period2 is considered. The returned value is from 0 to 1. For example:
matched_index(milk, period1="2018-12", period2="2019-12", type="prodID",interval=TRUE)
#> [1] 0.7258065matched_fig
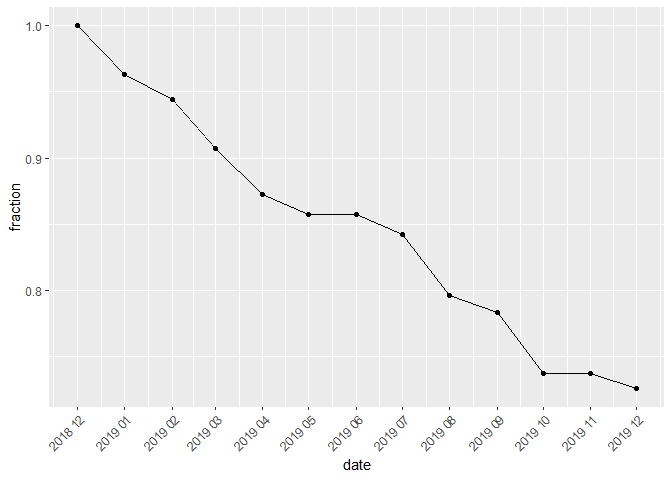
The function returns a data frame or a figure presenting the matched_index function calculated for the column defined by the type parameter and for each month from the considered time interval. The interval is set by the start and end parameters. The returned object (data frame or figure) depends on the value of the figure parameter. Examples:
matched_fig(milk, start="2018-12", end="2019-12", type="prodID")
matched_fig(milk, start="2018-12", end="2019-04", type="prodID", figure=FALSE)
#> date fraction
#> 1 2018-12 1.0000000
#> 2 2019-01 0.9629630
#> 3 2019-02 0.9444444
#> 4 2019-03 0.9074074
#> 5 2019-04 0.8727273products
This function detects and summarises available, matched, new and disappearing products on the basis of their prodIDs. It compares products from the base period (start) with products from the current period (end). It returns a list containing the following objects: details with prodIDs of available, matched, new and disappearing products, statistics with basic statistics for them and figure with a pie chart describing a contribution of matched, new and disappearing products in a set of available products. Please see the following example:
list<-products(milk, "2018-12","2019-12")
list$statistics
#> products volume shares
#> 1 available 61 100.00
#> 2 matched 47 77.05
#> 3 new 8 13.11
#> 4 disappearing 6 9.84list$figure products_fig
products_fig
This function returns a figure with plots of volume (or contributions) of available, matched, new as well as disappearing products. The User may control which groups of products are to be taken into consideration. Available options are available, matched, new and disappearing. Please follow the example:
products_fig(milk, "2018-12","2019-12",
fixed_base=TRUE, contributions=FALSE,
show=c("new","disappearing","matched","available")) prices
prices
The function returns prices (unit value) of products with a given ID (prodID column) and being sold in the time period indicated by the period parameter. The set parameter means a set of unique product IDs to be used for determining prices of sold products. If the set is empty the function returns prices of all products being available in the period. Please note that the function returns the price values for sorted prodIDs and in the absence of a given prodID in the data set, the function returns nothing (it does not return zero).To get prices (unit values) of all available milk products sold in July, 2019, please use:
prices(milk, period="2019-06")
#> [1] 8.700000 8.669455 1.890000 2.950000 1.990000 2.990000 2.834464
#> [8] 4.702051 2.163273 2.236250 2.810000 2.860000 2.400000 2.588644
#> [15] 3.790911 7.980000 64.057143 7.966336 18.972121 12.622225 9.914052
#> [22] 7.102823 3.180000 2.527874 1.810000 1.650548 2.790000 2.490000
#> [29] 2.590000 7.970131 9.901111 15.266667 19.502286 2.231947 2.674401
#> [36] 2.371819 2.490000 6.029412 6.441176 2.090000 1.990000 1.890000
#> [43] 1.450000 2.680000 2.584184 2.683688 2.390000 3.266000 2.813238quantities
The function returns quantities of products with a given ID (prodID column) and being sold in the time period indicated by the period parameter. The set parameter means a set of unique product IDs to be used for determining prices of sold products. If the set is empty the function returns quantities of all products being available in the period. Please note that the function returns the quantity values for sorted prodIDs and in the absence of a given prodID in the data set, the function returns nothing (it does not return zero). To get a data frame containing quantities of milk products with prodIDs: 400032, 71772 and 82919, and sold in July, 2019, please use:
quantities(milk, period="2019-06", set=c(400032, 71772, 82919), ID=TRUE)
#> # A tibble: 3 × 2
#> by q
#> <int> <dbl>
#> 1 71772 117
#> 2 82919 102
#> 3 400032 114.sales
The function returns values of sales of products with a given ID (prodID column) and being sold in the time period indicated by period parameter. The set parameter means a set of unique product IDs to be used for determining prices of sold products. If the set is empty the function returns values of sales of all products being available in the period (see also expenditures function which returns the expenditure values for sorted prodIDs). To get values of sales of milk products with prodIDs: 400032, 71772 and 82919, and sold in July, 2019, please use:
sales(milk, period="2019-06", set=c(400032, 71772, 82919))
#> [1] 913.71 550.14 244.80sales_groups
The function returns values of sales of products from one or more datasets or the corresponding barplot for these sales (if barplot is set to TRUE). Alternatively, it calculates the sale shares (if the shares parameter is set to TRUE). Please see also the sales_groups2 function. As an example, let us create 3 subgroups of milk products and let us find out their sale shares for the time interval: April, 2019 - July, 2019. We can obtain precise values for the given period:
ctg<-unique(milk$description)
categories<-c(ctg[1],ctg[2],ctg[3])
milk1<-dplyr::filter(milk, milk$description==categories[1])
milk2<-dplyr::filter(milk, milk$description==categories[2])
milk3<-dplyr::filter(milk, milk$description==categories[3])
sales_groups(datasets=list(milk1,milk2,milk3),start="2019-04", end="2019-07")
#> [1] 44400.76 152474.55 101470.76
sales_groups(datasets=list(milk1,milk2,milk3),start="2019-04", end="2019-07", shares=TRUE)
#> [1] 0.1488230 0.5110661 0.3401109or a barplot presenting these results:
sales_groups(datasets=list(milk1,milk2,milk3),start="2019-04", end="2019-07",
barplot=TRUE, shares=TRUE, names=categories)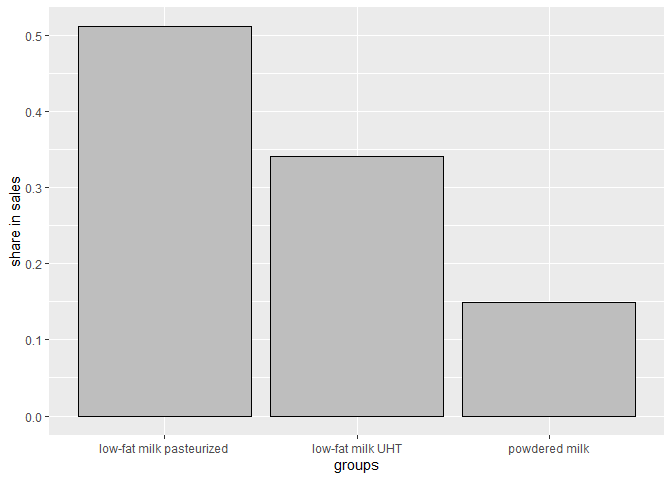 pqcor
pqcor
The function returns Pearson’s correlation coefficient for price and quantity of products with given IDs (defined by the set parameter) and sold in the period. If the set is empty, the function works for all products being available in the period. The figure parameter indicates whether the function returns a figure with a correlation coefficient (TRUE) or just a correlation coefficient (FALSE). For instance:
pqcor(milk, period="2019-05")
#> [1] -0.2047
pqcor(milk, period="2019-05",figure=TRUE)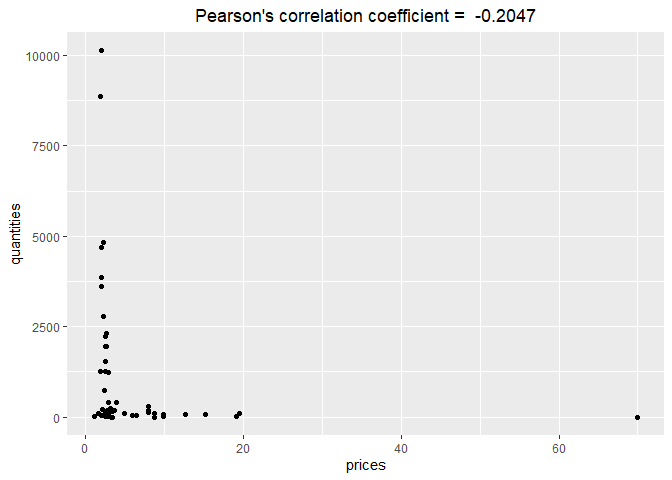 pqcor_fig
pqcor_fig
The function returns Pearson’s correlation coefficients between price and quantity of products with given IDs (defined by the set parameter) and sold in the time interval defined by the start and end parameters. If the set is empty the function works for all available products. Correlation coefficients are calculated for each month separately. Results are presented in tabular or graphical form depending on the figure parameter. Both cases are presented below:
pqcor_fig(milk, start="2018-12", end="2019-06", figure=FALSE)
#> date correlation
#> 1 2018-12 -0.1835
#> 2 2019-01 -0.1786
#> 3 2019-02 -0.1805
#> 4 2019-03 -0.1956
#> 5 2019-04 -0.1972
#> 6 2019-05 -0.2047
#> 7 2019-06 -0.2037
pqcor_fig(milk, start="2018-12", end="2019-06")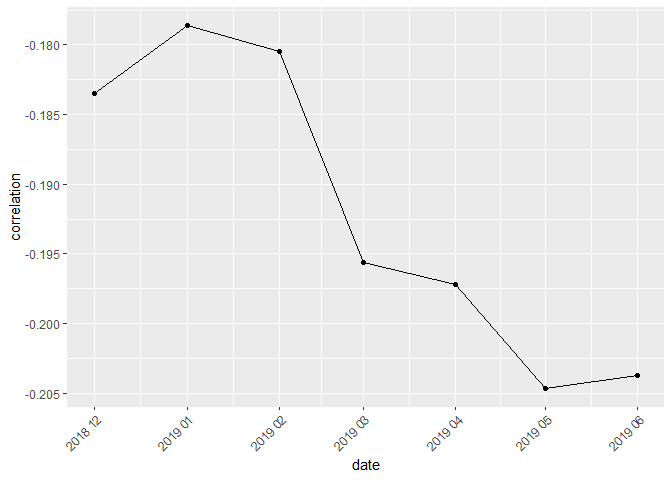 dissimilarity
dissimilarity
This function returns a value of the relative price (dSP) and/or quantity (dSQ) dissimilarity measure. In a special case, when the type parameter is set to pq, the function provides the value of dSPQ measure (relative price and quantity dissimilarity measure calculated as min(dSP,dSQ). For instance:
dissimilarity(milk, period1="2018-12",period2="2019-12",type="pq")
#> [1] 0.00004175192dissimilarity_fig
This function presents values of the relative price and/or quantity dissimilarity measure over time. The user can choose a benchmark period (defined by benchmark) and the type of dissimilarity measure is to be calculated (defined by type). The obtained results of dissimilarities over time can be presented in a dataframe form or via a figure (the default value of figure is TRUE which results a figure). For instance:
dissimilarity_fig(milk, start="2018-12",end="2019-12",type="pq",benchmark="start")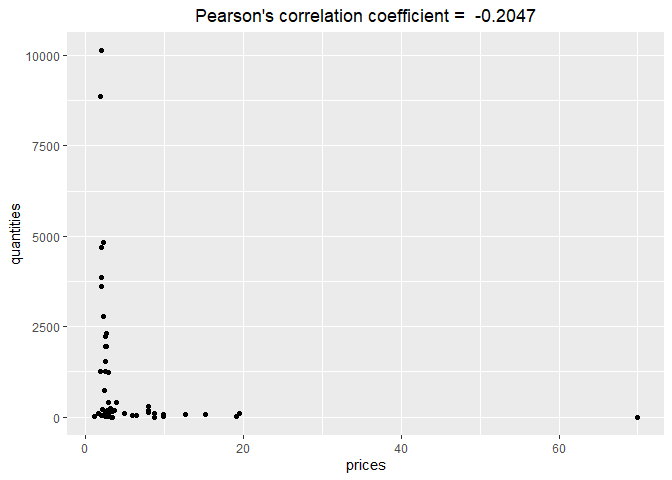 elasticity
elasticity
This function returns a value of the elasticity of substitution. If the method parameter is set to lm (it is a default value), the procedure of estimation solves the equation: LM(sigma)-CW(sigma)=0 numerically, where LM denotes the Lloyd-Moulton price index, the CW denotes a current weight counterpart of the Lloyd-Moulton price index, and sigma is the elasticity of substitution parameter, which is estimated. If the method parameter is set to f, the Fisher price index formula is used instead of the CW price index. If the method parameter is set to t, the Tornqvist price index formula is used instead of the CW price index. If the method parameter is set to w, the Walsh price index formula is used instead of the CW price index. If the method parameter is set to sv, the Sato-Vartia price index formula is used instead of the CW price index.The procedure continues until the absolute value of this difference is greater than the value of the ‘precision’ parameter. For example:
elasticity(coffee, start = "2018-12", end = "2019-01")
#> [1] 4.241791elasticity_fig
The function provides a data frame or a figure presenting elasticities of substitution calculated for time interval (see the figure parameter). The elasticities of substitution can be calculated for subsequent months or for a fixed base month (see the start parameter) and rest of months from the given time interval (it depends on the fixedbase parameter). The presented function is based on the elasticity function. For instance, to get elasticities of substitution calculated for milk products for subsequent months we run:
elasticity_fig (milk,start="2018-12",end="2019-04",figure=TRUE,
method=c("lm","f","sv"),names=c("LM","Fisher", "SV"))This package includes 8 functions for calculating the following bilateral unweighted price indices:
| Price Index | Function |
|---|---|
| BMW (2007) | bmw |
| Carli (1804) | carli |
| CSWD (1980,1992) | cswd |
| Dikhanov (2021, 2024) | dikhanov |
| Dutot (1738) | dutot |
| Jevons (1865) | jevons |
| Harmonic | harmonic |
| YBMD (2026) | ybmd |
Each of these functions returns a value (or vector of values) of the choosen unweighted bilateral price index depending on the interval parameter. If the interval parameter is set to TRUE, the function returns a vector of price index values without dates. To get information about both price index values and corresponding dates please see general functions: price_indices or final_index. None of these functions takes into account aggregating over outlets or product subgroups (to consider these types of aggregating please use the final_index function.) Below are examples of calculations for the Jevons index (in the second case a fixed base month is set to December 2018):
jevons(milk, start="2018-12", end="2020-01")
#> [1] 1.028223
jevons(milk, start="2018-12", end="2020-01", interval=TRUE)
#> [1] 1.0000000 1.0222661 1.0300191 1.0353857 1.0075504 1.0395393 0.9853148
#> [8] 1.0053100 1.0033727 1.0177604 1.0243906 1.0086291 1.0249373 1.0282234This package includes 35 functions for calculating the following bilateral weighted price indices:
| Price Index | Function |
|---|---|
| AG Mean (2009) | agmean |
| Banajree (1977) | banajree |
| Bialek (2012,2013) | bialek |
| Davies (1924) | davies |
| Drobisch (1871) | drobisch |
| Fisher (1922) | fisher |
| Geary-Khamis (1958,1970) | geary_khamis |
| Geo-Laspeyres | geolaspeyres |
| Geo-Lowe | geolowe |
| Geo-Paasche | geopaasche |
| Geo-Walsh | geowalsh |
| Geo-Young | geoyoung |
| Geo-hybrid (2020) | geohybrid |
| Harmonic log-change | hlc |
| Hybrid (2020) | hybrid |
| Laspeyres (1871) | laspeyres |
| Lehr (1885) | lehr |
| Lloyd-Moulton (1975,1996) | lloyd_moulton |
| Lowe | lowe |
| Marshall-Edgeworth (1887) | marshall_edgeworth |
| Paasche (1874) | paasche |
| Palgrave (1886) | palgrave |
| Sato-Vartia (1976) | sato_vartia |
| Stuvel (1957) | stuvel |
| Theil I | theil1 |
| Theil II | theil2 |
| Tornqvist (1936) | tornqvist |
| Vartia (1976) | vartia |
| Walsh (1901) | walsh |
| Walsh-Vartia | walsh_vartia |
| Young | young |
| Quadratic mean of order r price index | QMp |
| Implicit quadratic mean of order r price index | IQMp |
| Value Index | value_index |
| Unit Value Index | unit_value_index |
and the general quadratic mean of order r quantity index: QMq.
Each of these functions returns a value (or vector of values) of the choosen weighted bilateral price index depending on the interval parameter. If interval parameter is set to TRUE, the function returns a vector of price index values without dates. To get information about both price index values and corresponding dates please see general functions: price_indices or final_index. None of these functions takes into account aggregating over outlets or product subgroups (to consider these types of aggregating please use the final_index function.) Below are examples of calculations for the Fisher, the Lloyd-Moulton and the Lowe indices (in the last case, the fixed base month is set to December 2019 and the prior period is December 2018):
fisher(milk, start="2018-12", end="2020-01")
#> [1] 0.9615501
lloyd_moulton(milk, start="2018-12", end="2020-01", sigma=0.9)
#> [1] 0.9835069
lowe(milk, start="2019-12", end="2020-02", base="2018-12", interval=TRUE)
#> [1] 1.0000000 0.9880546 1.0024443The package also allows the User to calculate retrospective price indices. The retro_index function implements the correction or imputation approaches (see von Auer (2024) cited in the documentation) and also estimates the Diewert-Huwiler-Kohli-Hansen index (DHKH). For example, let us determine the retrospective DHKH index for the milk set:
retro_index(milk, start="2018-12", end="2019-12", formula="dhkh")
#> [1] 1.0000000 1.0040989 0.9989670 0.9947970 0.9949623 0.9896931 0.9929759
#> [8] 0.9903619 0.9972183 0.9997273 0.9768806 0.9966931 0.9868354This package includes 42 functions for calculating the following chain indices (weighted and unweighted):
| Price Index | Function |
|---|---|
| Chain BMW | chbmw |
| Chain Carli | chcarli |
| Chain CSWD | chcswd |
| Chain Dutot | chdutot |
| Chain Jevons | chjevons |
| Chain Harmonic | chharmonic |
| Chain Dikhanov | chdikhanov |
| Chain YBMD | chybmd |
| Chain AG Mean | chagmean |
| Chain Banajree | chbanajree |
| Chain Bialek | chbialek |
| Chain Davies | chdavies |
| Chain Drobisch | chdrobisch |
| Chain Fisher | chfisher |
| Chain Geary-Khamis | chgeary_khamis |
| Chain Geo-Laspeyres | chgeolaspeyres |
| Chain Geo-Lowe | chgeolowe |
| Chain Geo-Paasche | chgeopaasche |
| Chain Geo-Walsh | chgeowalsh |
| Chain Geo-Young | chgeoyoung |
| Chain Geo-hybrid | chgeohybrid |
| Chain harmonic log-change | chhlc |
| Chain Hybrid | chhybrid |
| Chain Laspeyres | chlaspeyres |
| Chain Lehr | chlehr |
| Chain Lloyd-Moulton | chlloyd_moulton |
| Chain Lowe | chlowe |
| Chain Marshall-Edgeworth | chmarshall_edgeworth |
| Chain Paasche | chpaasche |
| Chain Palgrave | chpalgrave |
| Chain Sato-Vartia | chsato_vartia |
| Chain Stuvel | chstuvel |
| Chain Theil I | chtheil1 |
| Chain Theil II | chtheil2 |
| Chain Tornqvist | chtornqvist |
| Chain Vartia | chvartia |
| Chain Walsh | chwalsh |
| Chain Walsh-Vartia | chwalsh_vartia |
| Chain Young | chyoung |
| Chain quadratic mean of order r price index | chQMp |
| Chain implicit quadratic mean of order r price index | chIQMp |
| Chain quadratic mean of order r quantity index | chQMq |
Each time, the interval parameter has a logical value indicating whether the function is to compare the research period defined by end to the base period defined by start (then interval is set to FALSE and it is a default value) or all fixed base indices are to be calculated. In this second case, all months from the time interval <start,end> are considered and start defines the base period (interval is set to TRUE). Here are examples for the Fisher chain index:
chfisher(milk, start="2018-12", end="2020-01")
#> [1] 0.9618094
chfisher(milk, start="2018-12", end="2020-01", interval=TRUE)
#> [1] 1.0000000 1.0021692 1.0004617 0.9862756 0.9944042 0.9915704 0.9898026
#> [8] 0.9876325 0.9981591 0.9968851 0.9786428 0.9771951 0.9874251 0.9618094This package includes 22 functions for calculating multilateral price indices and one additional and general function (QU) which calculates the quality adjusted unit value index, i.e.:
| Price Index | Function |
|---|---|
| CCDI | ccdi |
| GEKS | geks |
| WGEKS | wgeks |
| GEKS-J | geksj |
| GEKS-W | geksw |
| GEKS-L | geksl |
| WGEKS-L | wgeksl |
| GEKS-GL | geksgl |
| WGEKS-GL | wgeksgl |
| GEKS-AQU | geksaqu |
| WGEKS-AQU | wgeksaqu |
| GEKS-AQI | geksaqi |
| WGEKS-AQI | wgeksaqi |
| GEKS-GAQI | geksgaqi |
| GEKS-IQM | geksiqm |
| GEKS-QM | geksqm |
| GEKS-LM | gekslm |
| WGEKS-GAQI | wgeksgaqi |
| Geary-Khamis | gk |
| Quality Adjusted Unit Value | QU |
| Time Product Dummy | tpd |
| Unweighted Time Product Dummy | utpd |
| SPQ | SPQ |
The above-mentioned 21 multilateral formulas (the SPQ index is an exception) consider the time window defined by the wstart and window parameters, where window is a length of the time window (typically multilateral methods are based on a 13-month time window). It measures the price dynamics by comparing the end period to the start period (both start and end must be inside the considered time window). To get information about both price index values and corresponding dates, please see functions: price_indices or final_index. These functions do not take into account aggregating over outlets or product subgroups (to consider these types of aggregating please use function: final_index ). Here are examples for the GEKS formula (see documentation):
geks(milk, start="2019-01", end="2019-04",window=10)
#> [1] 0.9912305
geksl(milk, wstart="2018-12", start="2019-03", end="2019-05")
#> [1] 1.002251The user may decompose the GEKS-type indices. The m_decomposition function returns multiplicative decompositions of the selected GEKS-type indices. For instance:
milk.<-milk
milk.$prodID<-milk.$description
m_decomposition(milk., start="2018-12", end="2019-12",
formula=c("geks","ccdi"))$multiplicative
#> product GEKS CCDI
#> 1 full-fat milk UHT 0.9901247 0.9901350
#> 2 full-fat milk pasteurized 0.9966904 0.9966895
#> 3 goat milk 0.9999800 0.9999800
#> 4 low-fat milk UHT 1.0018916 1.0018830
#> 5 low-fat milk pasteurized 1.0035170 1.0035052
#> 6 powdered milk 1.0064838 1.0065987
#> 7 index value (product) 0.9986050 0.9987082The QU function returns a value of the quality adjusted unit value index (QU index) for the given set of adjustment factors. An additional v parameter is a data frame with adjustment factors for at least all matched prodIDs. It must contain two columns: prodID with unique product IDs and value with corresponding adjustment factors (see documentation). The following example starts from creating a data frame which includes sample adjusted factors:
prodID<-base::unique(milk$prodID)
values<-stats::runif(length(prodID),1,2)
v<-data.frame(prodID,values)
head(v)
#> prodID values
#> 1 14215 1.997964
#> 2 14216 1.442881
#> 3 15404 1.938168
#> 4 17034 1.795812
#> 5 34540 1.451062
#> 6 51583 1.236759and the next step is calculating the QU index which compares December 2019 to December 2018:
QU(milk, start="2018-12", end="2019-12", v)
#> [1] 1.031549This package includes 21 functions for calculating splice indices:
| Price Index | Function |
|---|---|
| Splice CCDI | ccdi_splcie |
| Splice GEKS | geks_splice |
| Splice weighted GEKS | wgeks_splice |
| Splice GEKS-J | geksj_splice |
| Splice GEKS-W | geksw_splice |
| Splice GEKS-L | geksl_splice |
| Splice weighted GEKS-L | wgeksl_splice |
| Splice GEKS-GL | geksgl_splice |
| Splice weighted GEKS-GL | wgeksgl_splice |
| Splice GEKS-AQU | geksaqu_splice |
| Splice weighted GEKS-AQU | wgeksaqu_splice |
| Splice GEKS-AQI | geksaqi_splice |
| Splice weighted GEKS-AQI | wgeksaqi_splice |
| Splice GEKS-GAQI | geksgaqi_splice |
| Splice weighted GEKS-GAQI | wgeksgaqi_splice |
| Splice GEKS-IQM | geksiqm_splice |
| Splice GEKS-QM | geksqm_splice |
| Splice GEKS-LM | gekslm_splice |
| Splice Geary-Khamis | gk_splice |
| Splice Time Product Dummy | tpd_splice |
| Splice unweighted Time Product Dummy | utpd_splice |
These functions return a value (or values) of the selected multilateral price index extended by using window splicing methods (defined by the splice parameter). Available splicing methods are: movement splice, window splice, half splice, mean splice and their additional variants: window splice on published indices (WISP), half splice on published indices (HASP) and mean splice on published indices (see documentation). The first considered time window is defined by the start and window parameters, where window is a length of the time window (typically multilateral methods are based on a 13-month time window). Functions measure the price dynamics by comparing the end period to the start period, i.e. if the time interval <start, end> exceeds the defined time window then splicing methods are used. If the interval parameter is set to TRUE, then all fixed base multilateral indices are presented (the fixed base month is defined by start). To get information about both price index values and corresponding dates, please see functions: price_indices or final_index. These functions do not take into account aggregating over outlets or product subgroups (to consider these types of aggregating, please use the final_index function). For instance, let us calculate the extended Time Product Dummy index by using the half splice method with a 10-month time window:
tpd_splice(milk, start="2018-12", end="2020-02",window=10,splice="half",interval=TRUE)
#> [1] 1.0000000 1.0038893 1.0000284 0.9837053 0.9954196 0.9924919 0.9913655
#> [8] 0.9866847 0.9998615 0.9949000 0.9806788 0.9808493 0.9888003 0.9628623
#> [15] 1.0021956This package includes 21 functions for calculating extensions of multilateral indices by using the Fixed Base Monthly Expanding Window (FBEW) method:
| Price Index | Function |
|---|---|
| FBEW CCDI | ccdi_fbew |
| FBEW GEKS | geks_fbew |
| FBEW WGEKS | wgeks_fbew |
| FBEW GEKS-J | geksj_fbew |
| FBEW GEKS-W | geksw_fbew |
| FBEW GEKS-L | geksl_fbew |
| FBEW WGEKS-L | wgeksl_fbew |
| FBEW GEKS-GL | geksgl_fbew |
| FBEW WGEKS-GL | wgeksgl_fbew |
| FBEW GEKS-AQU | geksaqu_fbew |
| FBEW WGEKS-AQU | wgeksaqu_fbew |
| FBEW GEKS-AQI | geksaqi_fbew |
| FBEW WGEKS-AQI | wgeksaqi_fbew |
| FBEW GEKS-GAQI | geksgaqi_fbew |
| FBEW WGEKS-GAQI | wgeksgaqi_fbew |
| FBEW GEKS-QM | geksqm_fbew |
| FBEW GEKS-IQM | geksiqm_fbew |
| FBEW GEKS-LM | gekslm_fbew |
| FBEW Geary-Khamis | gk_fbew |
| FBEW Time Product Dummy | tpd_fbew |
| FBEW unweighted Time Product Dummy | utpd_fbew |
These functions return a value (or values) of the selected multilateral price index extended by using the FBEW method. The FBEW method uses a time window with a fixed base month every year (December). The window is enlarged every month with one month in order to include information from a new month. The full window length (13 months) is reached in December of each year. These functions measure the price dynamics between the end and start periods. A month of the start parameter must be December (see documentation). If the distance between end and start exceeds 13 months, then internal Decembers play a role of chain-linking months. To get information about both price index values and corresponding dates please see functions: price_indices or final_index. These functions do not take into account aggregating over outlets or product subgroups (to consider these types of aggregating, please use the final_index function). For instance, let us calculate the extended GEKS index by using the FBEW method. Please note that December 2019 is the chain-linking month, i.e.:
geks_fbew(milk, start="2018-12", end="2020-03")
#> [1] 0.9891602
geks_fbew(milk, start="2018-12", end="2019-12")*
geks_fbew(milk, start="2019-12", end="2020-03")
#> [1] 0.9891602This package includes 21 functions for calculating extensions of multilateral indices by using the Fixed Base Moving Window (FBMW) method:
| Price Index | Function |
|---|---|
| FBMW CCDI | ccdi_fbmw |
| FBMW GEKS | geks_fbmw |
| FBMW WGEKS | wgeks_fbmw |
| FBMW GEKS-J | geksj_fbmw |
| FBMW GEKS-W | geksw_fbmw |
| FBMW GEKS-L | geksl_fbmw |
| FBMW WGEKS-L | wgeksl_fbmw |
| FBMW GEKS-GL | geksgl_fbmw |
| FBMW WGEKS-GL | wgeksgl_fbmw |
| FBMW GEKS-AQU | geksaqu_fbmw |
| FBMW WGEKS-AQU | wgeksaqu_fbmw |
| FBMW GEKS-AQI | geksaqi_fbmw |
| FBMW WGEKS-AQI | wgeksaqi_fbmw |
| FBMW GEKS-GAQI | geksgaqi_fbmw |
| FBMW WGEKS-GAQI | wgeksgaqi_fbmw |
| FBMW GEKS-IQM | geksiqm_fbmw |
| FBMW GEKS-QM | geksqm_fbmw |
| FBMW GEKS-LM | gekslm_fbmw |
| FBMW Geary-Khamis | gk_fbmw |
| FBMW Time Product Dummy | tpd_fbmw |
| FBMW unweighted Time Product Dummy | utpd_fbmw |
These functions return a value (or values) of the selected multilateral price index extended by using the FBMW method. They measure the price dynamics between the end and start periods and it uses a 13-month time window with a fixed base month taken as year(end)-1. If the distance between end and start exceeds 13 months, then internal Decembers play a role of chain-linking months. A month of the start parameter must be December (see documentation). To get information about both price index values and corresponding dates, please see functions: price_indices or final_index. These functions do not take into account aggregating over outlets or product subgroups (to consider these types of aggregating, please use the final_index function). For instance, let us calculate the extended CCDI index by using the FBMW method. Please note that December 2019 is the chain-linking month, i.e.:
ccdi_fbmw(milk, start="2018-12", end="2020-03")
#> [1] 0.9874252
ccdi_fbmw(milk, start="2018-12", end="2019-12")*
ccdi_fbmw(milk, start="2019-12", end="2020-03")
#> [1] 0.9874252This package includes 3 general functions for price index calculation. The start and end parameters indicate the base and the research period respectively. These function provide value or values (depending on the interval parameter) of the selected price index formula or formulas. If the interval parameter is set to TRUE then it returns a data frame with two columns: dates and index values. Function price_indices does not take into account aggregating over outlets or product subgroups and to consider these types of aggregating, please use function: final_index.
price_indices
This function allows us to compare many price index formulas by using one command. The general character of this function mean that, for instance, your one command may calculate two CES indices for two different values of sigma parameter (the elasticity of substitution) or you can select several splice indices and calculate them by using different window lengths and different splicing method. You can control names of columns in the resulting data frame by defining additional parameters: names. Please note that this function is not the most general in the package, i.e. all selected price indices are calculated for the same data set defined by the data parameter and the aggregation over subgroups or outlets are not taken into consideration here (to consider it, please use function: final_index).
For instance:
price_indices(milk,
start = "2018-12", end = "2019-12",
formula=c("geks","ccdi","hybrid","fisher",
"QMp","young","geksl_fbew"),
window = c(13, 13),
base = c("2019-03", "2019-03"),
r=c(3), interval=TRUE)
#> time geks ccdi hybrid fisher QMp young
#> 1 2018-12 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000 1.0000000
#> 2 2019-01 1.0020172 1.0018004 0.9967071 1.0021692 1.0025266 0.9982428
#> 3 2019-02 1.0001330 0.9997978 1.0009266 0.9983528 0.9983839 1.0005565
#> 4 2019-03 0.9839258 0.9840643 0.9737613 0.9868188 0.9866552 0.9766453
#> 5 2019-04 0.9936427 0.9932822 0.9861536 0.9954079 0.9956790 0.9875892
#> 6 2019-05 0.9899234 0.9898612 0.9866800 0.9904548 0.9905572 0.9874894
#> 7 2019-06 0.9889829 0.9888433 0.9808391 0.9906674 0.9908235 0.9827443
#> 8 2019-07 0.9862652 0.9864494 0.9889462 0.9848588 0.9845825 0.9893828
#> 9 2019-08 0.9981114 0.9978518 1.0012679 0.9987586 0.9989635 1.0005086
#> 10 2019-09 0.9952078 0.9951481 0.9985214 0.9959955 0.9962294 0.9976441
#> 11 2019-10 0.9776535 0.9773428 0.9747949 0.9767235 0.9770339 0.9746506
#> 12 2019-11 0.9805743 0.9815496 0.9948243 0.9771107 0.9762389 0.9943300
#> 13 2019-12 0.9876664 0.9876167 0.9952270 0.9868354 0.9868723 0.9939052
#> geksl_fbew
#> 1 1.0000000
#> 2 1.0021692
#> 3 0.9964178
#> 4 0.9856119
#> 5 0.9914299
#> 6 0.9884677
#> 7 0.9873196
#> 8 0.9874639
#> 9 0.9957917
#> 10 0.9951035
#> 11 0.9739414
#> 12 0.9882475
#> 13 0.9844756or
price_indices(coffee,
start = "2018-12", end = "2019-12",
formula=c("laspeyres","paasche","fisher"),
interval=FALSE)
#> price_index value
#> 1 laspeyres 1.0167511
#> 2 paasche 0.9863043
#> 3 fisher 1.0014120final_index
This general function returns a value or values of the selected final price index for the selected type of aggregation of partial results. If the interval parameter is set to TRUE, then it returns a data frame where its first column indicates dates and the remaining columns show corresponding values of all selected price index. A final price index formula can be any index formula which is available in the PriceIdices packages (bilateral or multilateral). The formula used for aggregating partial index results is selected by the aggr parameter and the User decides on directions of aggregation (see outlets and groups parameters).
Example. Let us calculate the final Fisher price index (with Laspeyres-type aggregation over outlets and product subgroups) for the data set on milk
final_index(milk, start = "2018-12", end = "2019-12",
formula = "fisher", groups = TRUE, outlets = TRUE,
aggr = "laspeyres", by = "description",
interval = TRUE)
#> time final fisher
#> 1 2018-12 1.0000000
#> 2 2019-01 1.0043285
#> 3 2019-02 0.9994987
#> 4 2019-03 0.9909980
#> 5 2019-04 0.9955766
#> 6 2019-05 0.9922104
#> 7 2019-06 0.9910091
#> 8 2019-07 0.9862940
#> 9 2019-08 0.9981004
#> 10 2019-09 0.9978900
#> 11 2019-10 0.9764887
#> 12 2019-11 0.9837980
#> 13 2019-12 0.9871036This package includes two functions for a simple graphical comparison of price indices and two functions for calculating distances between indices. The first one, i.e. compare_indices_df, is based on the syntax of the price_indices function and thus it allows us to compare price indices calculated on the same data set. The second function, i.e. compare_indices_list, has a general character since its first argument is a list of data frames which contain results obtained by using the price_indices or final_index functions. The third one, i.e. compare_distances, calculates (average) distances between price indices, i.e. the mean absolute distance or root mean square distance is calculated. The next function, compare_to_target, allows to compute distances between indices from the selected index group and the indicated target price index. The last function, compare_indices_jk, presents a comparison of selected indices obtained by using the jackknife method.
compare_indices_df and compare_indices_list
These functions return a figure with plots of selected price indices, which are provided as a data frame (compare_indices_df) or a list of data frames (compare_indices_list). For instance, let us compare the Laspeyres and Paasche indices calculated for the data set on milk:
df<-price_indices(milk, start = "2018-12", end = "2019-12",
formula=c("laspeyres", "fisher"), interval = TRUE)
compare_indices_df(df)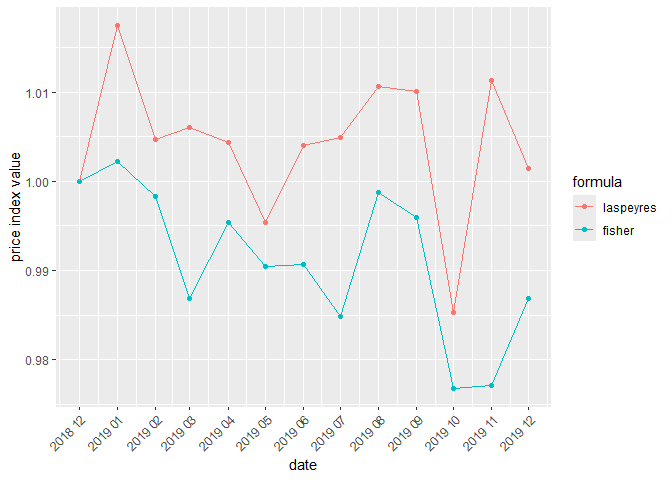
Now, let us compare the impact of the aggregating over outlets on the price index results (e.g. the Laspeyres formula is the assumed aggregating method). For this purpose, let us calculate the Fisher price index in two cases: case1 without the above-mentioned aggregation and case2 which considers that aggregation. We use the milk dataset and the yearly time interval:
case1<-price_indices(milk, start="2018-12",end="2019-12",
formula="fisher", interval=TRUE)
case2<-final_index(milk, start="2018-12", end="2019-12",
formula="fisher",
outlets=TRUE,
aggr = "laspeyres",
interval=TRUE)The comparison of obtained results can be made as follows:
compare_indices_list(data=list(case1, case2),
names=c("Fisher without aggregation",
"Fisher with aggregation"))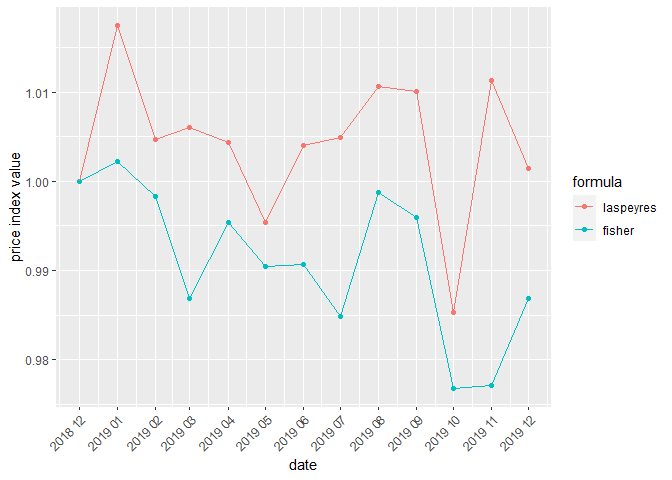
compare_distances
The function calculates average distances between price indices and it returns a data frame with these values for each pair of price indices. The main data parameter is a data frame containing values of indices which are to be compared. The measure parameter specifies what measure should be used to compare the indexes. Possible parameter values are: “MAD” (Mean Absolute Distance) or “RMSD” (Root Mean Square Distance). The results may be presented in percentage points (see the pp parameter) and we can control how many decimal places are to be used in the presentation of results (see the prec parameter).
For instance, let us compare the Jevons, Dutot and Carli indices calculated for the milk data set and for the time interval: December 2018 - December 2019. Let us use the MAD measure for these comparisons:
#Creating a data frame with unweighted bilateral index values
df<-price_indices(milk,
formula=c("jevons","dutot","carli"),
start="2018-12",
end="2019-12",
interval=TRUE)
#Calculating average distances between indices (in p.p)
compare_distances(df)
#> jevons dutot carli
#> jevons 0.000 2.482 2.093
#> dutot 2.482 0.000 4.420
#> carli 2.093 4.420 0.000compare_to_target
The function calculates average distances between considered price indices and the target price index and it returns a data frame with: average distances on the basis of all values of compared indices (distance column), average semi-distances on the basis of values of compared indices which overestimate the target index values (distance_upper column) and average semi-distances on the basis of values of compared indices which underestimate the target index values (distance_lower column).
For instance, let us compare the Jevons, Laspeyres, Paasche and Walsh price indices (calculated for the milk data set and for the time interval: December 2018 - December 2019) with the target Fisher price index:
#Creating a data frame with example bilateral indices
df<-price_indices(milk,
formula=c("jevons","laspeyres","paasche","walsh"),
start="2018-12",end="2019-12",interval=TRUE)
#Calculating the target Fisher price index
target_index<-fisher(milk,start="2018-12",end="2019-12",interval=TRUE)
#Calculating average distances between considered indices and the Fisher index (in p.p)
compare_to_target(df,target=target_index)
#> index distance distance_lower distance_upper
#> 1 jevons 2.759 0.045 2.714
#> 2 laspeyres 1.429 0.000 1.429
#> 3 paasche 1.403 1.403 0.000
#> 4 walsh 0.174 0.113 0.061compare_indices_jk
This function presents a comparison of selected indices obtained by using the jackknife method. In particular, it returns a list with four elements: iterations, which is a data frame with basic characteristics of the calculated iteration index values (means, standard deviations, coefficients of variation and results for all sample), pseudovalues, which is a data frame with basic characteristics of the calculated index pseudovalues obtained in the jackknife procedure (i.e. the jackknife estimators and their standard deviations and coefficients of variation), figure_iterations which presents a box-plot for the calculated iteration index values, and figure_pseudovalues which presents a box-plot for the calculated index pseudovalues obtained in the jackknife procedure. Please follow the example, in which the Jevons, Fisher and GEKS indices are compared by using the jackknife method:
#creating a list with jackknife results
comparison<-compare_indices_jk(milk,
formula=c("jevons","fisher","geks"),
start="2018-12",
end="2019-12",
window=c(13),
names=c("Jevons","Fisher","GEKS"),
by="retID",
title_iterations="Box-plots for iteration values",
title_pseudovalues="Box-plots for pseudovalues")
#displaying a data frame with basic characteristics of the calculated iteration index values
comparison$iterations
#> # A tibble: 3 × 5
#> variable mean_iterations sd_iterations cv_iterations all_sample
#> <fct> <dbl> <dbl> <dbl> <dbl>
#> 1 Jevons 1.02 0.00668 0.00655 1.02
#> 2 Fisher 0.987 0.00108 0.00110 0.987
#> 3 GEKS 0.988 0.000909 0.000921 0.988#displaying a data frame with basic characteristics of the calculated index pseudovalues obtained in the jackknife procedure
comparison$pseudovalues
#> # A tibble: 3 × 4
#> variable jk_estimator sd_jk_estimator cv_jk
#> <fct> <dbl> <dbl> <dbl>
#> 1 Jevons 1.05 0.0267 0.0255
#> 2 Fisher 0.987 0.00433 0.00439
#> 3 GEKS 0.988 0.00364 0.00368#displaying box-plotes created for the calculated iteration index values
comparison$figure_iterations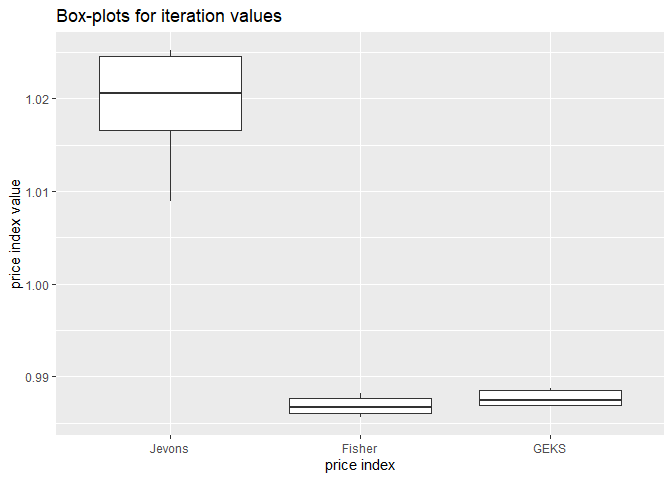
#displaying box-plotes created for the calculated index pseudovalues obtained in the jackknife procedure
comparison$figure_pseudovaluesThere are four package functions for calculating price and quantity indicators. The bennet function returns the (bilateral) Bennet price and quantity indicators and optionally also the price and quantity contributions of individual products. The mbennet function returns the multilateral (transitive) Bennet price and quantity indicators and optionally also the price and quantity contributions of individual products. The montgomery function returns the (bilateral) Montgomery price and quantity indicators and optionally also the price and quantity contributions of individual products. The mmontgomery function returns the multilateral (transitive) Montgomery price and quantity indicators and optionally also the price and quantity contributions of individual products.For instance, the following command calculates the Bennet price and quantity indicators for milk products:
bennet(milk, start = "2018-12", end = "2019-12", interval=TRUE)
#> time Value_difference Price_indicator Quantity_indicator
#> 1 2019-01 -31942.53 628.05 -32570.58
#> 2 2019-02 -35995.09 -175.29 -35819.80
#> 3 2019-03 -42158.05 -3810.15 -38347.90
#> 4 2019-04 -56934.44 -2427.25 -54507.20
#> 5 2019-05 -50961.52 -2580.91 -48380.61
#> 6 2019-06 -48842.58 -2396.05 -46446.53
#> 7 2019-07 -33974.27 -3232.63 -30741.64
#> 8 2019-08 -37962.80 4500.45 -42463.26
#> 9 2019-09 -33833.42 -1092.32 -32741.09
#> 10 2019-10 -35001.60 -1665.10 -33336.50
#> 11 2019-11 -16928.94 2313.87 -19242.81
#> 12 2019-12 9859.34 -2151.48 12010.83where price and quantity contributions of each subgroups of milk products can be obtained as follows:
milk$prodID<-milk$description
bennet(milk, start = "2018-12", end = "2019-12", contributions = TRUE)
#> prodID value_differences price_contributions
#> 1 full-fat milk UHT 8767.34 -1927.29
#> 2 full-fat milk pasteurized -711.57 -633.65
#> 3 goat milk -602.29 -4.10
#> 4 low-fat milk UHT -1525.62 369.49
#> 5 low-fat milk pasteurized 1421.39 647.66
#> 6 powdered milk 2510.09 1444.46
#> quantity_contributions
#> 1 10694.63
#> 2 -77.92
#> 3 -598.18
#> 4 -1895.11
#> 5 773.73
#> 6 1065.63The following command calculates the Montgomery price and quantity indicators for coffee products:
montgomery(coffee, start = "2018-12", end = "2019-12", interval=TRUE)
#> time Value_difference Price_indicator Quantity_indicator
#> 1 2019-01 -468907.15 -9147.81 -459759.34
#> 2 2019-02 -494284.67 20407.49 -514692.16
#> 3 2019-03 -397279.68 -14075.89 -383203.79
#> 4 2019-04 -354810.23 18916.05 -373726.28
#> 5 2019-05 -504512.39 35906.94 -540419.33
#> 6 2019-06 -461707.07 132177.82 -593884.89
#> 7 2019-07 -423952.45 110250.18 -534202.63
#> 8 2019-08 -275624.60 126281.93 -401906.53
#> 9 2019-09 -346025.72 151139.77 -497165.49
#> 10 2019-10 -310279.89 135645.97 -445925.86
#> 11 2019-11 -260821.56 44782.99 -305604.55
#> 12 2019-12 8945.14 75463.07 -66517.93where price and quantity contributions of each subgroups of coffee products can be obtained as follows:
coffee$prodID<-coffee$description
montgomery(coffee, start = "2018-12", end = "2019-12", contributions = TRUE)
#> prodID value_differences price_contributions quantity_contributions
#> 1 coffee beans 121932.78 -6100.99 128033.77
#> 2 ground coffee -70172.42 -14307.11 -55865.31
#> 3 instant coffee -42815.22 14483.76 -57298.98These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.