The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
RcppCensSpatial
packageThe RcppCensSpatial package fits a spatial censored
linear regression model using the Expectation-Maximization (EM)
(Dempster, Laird, and Rubin 1977), Stochastic Approximation EM (SAEM)
(Delyon, Lavielle, and Moulines 1999), or Monte Carlo EM (MCEM) (Wei and
Tanner 1990) algorithm. These algorithms are widely used to compute the
maximum likelihood (ML) estimates for incomplete data problems. The EM
algorithm computes the ML estimates when a closed expression for the
conditional expectation of the complete-data log-likelihood function is
available. In the MCEM algorithm, the conditional expectation is
substituted by a Monte Carlo approximation based on many independent
simulations of the partially observed data. In contrast, the SAEM
algorithm splits the E-step into simulation and integration steps.
This package also approximates the standard error of the estimates using the method developed by Louis (1982) and supports missing values on the dependent variable. Moreover, it has a function that performs spatial prediction in new locations. It also allows computing the covariance matrix and the distance matrix. For more information about the model formulation and estimation, please see Ordoñez et al. (2018) and Valeriano et al. (2021).
The RcppCensSpatial library provides the following
functions:
CovMat: computes the spatial covariance matrix.dist2Dmatrix: computes the Euclidean distance matrix
for a set of coordinates.EM.sclm: fits a spatial censored linear regression
model via the EM algorithm.MCEM.sclm: fits a spatial censored linear regression
model via the MCEM algorithm.SAEM.sclm: fits a spatial censored linear regression
model via the SAEM algorithm.predict.sclm: performs spatial prediction in a set of
new locations.rCensSp: simulates censored spatial data for an
established censoring rate.print, summary, predict, and
plot functions also work for the sclm
class.
Next, we will describe how to install the package and use all the previous methods in an artificial example.
The released version of RcppCensSpatial from CRAN can be installed with:
install.packages("RcppCensSpatial")In the following example, we simulate a dataset of length n = 220 from the spatial linear regression model considering three covariates and the exponential correlation function to deal with the variation between spatial points. In order to evaluate the prediction accuracy, the dataset is train-test split. The training data consists of 200 observations, with 5% censored to the left, while the testing data contains 20 observations.
library(RcppCensSpatial)
set.seed(12341)
n = 220
x = cbind(1, runif(n), rnorm(n))
coords = round(matrix(runif(2*n, 0, 15), n, 2), 5)
dat = rCensSp(beta=c(1,2,-1), sigma2=1, phi=4, nugget=0.50, x=x, coords=coords,
cens='left', pcens=.05, npred=20, cov.model="exponential")
# Proportion of censoring
table(dat$Data$ci)
#>
#> 0 1
#> 190 10For comparison purposes, we fit the spatial censored linear model for
the simulated data using three approaches: EM, MCEM, and SAEM algorithm.
Each method considers the same maximum number of iterations
MaxIter=300, and the spatial correlation function used in
the simulation process, i.e., type='exponential', the
default value. Other types of spatial correlation functions available
are 'matern', 'gaussian', and
'pow.exp'.
data1 = dat$Data
# EM estimation
fit1 = EM.sclm(data1$y, data1$x, data1$ci, data1$lcl, data1$ucl, data1$coords,
phi0=3, nugget0=1, MaxIter=300)
fit1$tab
#> beta0 beta1 beta2 sigma2 phi tau2
#> 0.6959 1.7894 -0.9477 1.2032 4.3018 0.3824
#> s.e. 0.4848 0.2027 0.0592 0.5044 2.2872 0.0793
# MCEM estimation
fit2 = MCEM.sclm(data1$y, data1$x, data1$ci, data1$lcl, data1$ucl, data1$coords,
phi0=3, nugget0=1, MaxIter=300, nMax=1000)
fit2$tab
#> beta0 beta1 beta2 sigma2 phi tau2
#> 0.6952 1.7896 -0.9476 1.2069 4.3216 0.3828
#> s.e. 0.4868 0.2025 0.0592 0.5121 2.3144 0.0793
# SAEM estimation
fit3 = SAEM.sclm(data1$y, data1$x, data1$ci, data1$lcl, data1$ucl, data1$coords,
phi0=3, nugget0=1, M=10)
fit3$tab
#> beta0 beta1 beta2 sigma2 phi tau2
#> 0.6959 1.7883 -0.9471 1.2060 4.3207 0.3811
#> s.e. 0.4865 0.2021 0.0590 0.5096 2.3125 0.0791Note that the estimates obtained for each parameter are similar and close to the true parameter value, except for the first regression coefficient, which was estimated close to 0.70, while the true value was equal to 1.
Moreover, generic functions print and
summary return some results of the fit for the
sclm class, such as the estimated parameters, standard
errors, the effective range, the information criteria, and some
convergence details.
print(fit3)
#> ----------------------------------------------------------------
#> Spatial Censored Linear Regression Model
#> ----------------------------------------------------------------
#> Call:
#> SAEM.sclm(y = data1$y, x = data1$x, ci = data1$ci, lcl = data1$lcl,
#> ucl = data1$ucl, coords = data1$coords, phi0 = 3, nugget0 = 1,
#> M = 10)
#>
#> Estimated parameters:
#> beta0 beta1 beta2 sigma2 phi tau2
#> 0.6959 1.7883 -0.9471 1.2060 4.3207 0.3811
#> s.e. 0.4865 0.2021 0.0590 0.5096 2.3125 0.0791
#>
#> The effective range is 12.9436 units.
#>
#> Model selection criteria:
#> Loglik AIC BIC
#> Value -251.323 514.645 534.435
#>
#> Details:
#> Number of censored/missing values: 10
#> Convergence reached?: TRUE
#> Iterations: 161 / 300
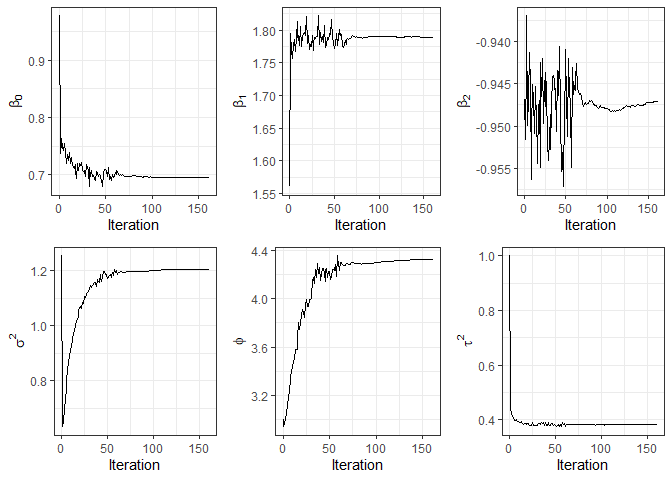
#> Processing time: 37.2335 secsOn the other hand, the function plot provides
convergence graphics for the parameters.
plot(fit3)
Now, we compute the predicted values for each fitted model for the testing data and compare the mean squared prediction error (MSPE).
data2 = dat$TestData
pred1 = predict(fit1, data2$coords, data2$x)
pred2 = predict(fit2, data2$coords, data2$x)
pred3 = predict(fit3, data2$coords, data2$x)
# Cross-validation
mean((data2$y - pred1$predValues)^2)
#> [1] 1.595305
mean((data2$y - pred2$predValues)^2)
#> [1] 1.591421
mean((data2$y - pred3$predValues)^2)
#> [1] 1.594899These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.