The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
The goal of StempCens is to estimates the parameters of
a censored or missing data in spatio-temporal models using the SAEM
algorithm (Delyon, Lavielle, and Moulines 1999). This algorithm is a
stochastic approximation of the widely used EM algorithm and an
important tool for models in which the E-step does not have an analytic
form. Besides the expressions obtained to estimate the parameters to the
proposed model, we include the calculations for the observed information
matrix using the method developed by Louis (1982). To examine the
performance of the fitted model, case-deletion measure are provided (see
also Cook 1977; Zhu et al. 2001). Moreover, it computes the
spatio-temporal covariance matrix and the effective range for an
isotropic spatial correlation function.
You can install the released version of StempCens from CRAN with:
install.packages("StempCens")StempCens package provides five functions:
CovarianceM: Computes the spatio-temporal covariance
matrix for balanced data.EffectiveRange: Computes the effective range for an
isotropic spatial correlation function.EstStempCens: Returns the maximum likelihood estimates
of the unknown parameters.PredStempCens: Performs spatio-temporal prediction in a
set of new spatial locations for fixed time points.CrossStempCens: Performs cross-validation, which
measure the performance of the predictive model on new test
dataset.DiagStempCens: Returns measures and graphics for
diagnostic analysis.This is a basic example which shows you how to solve a problem using
functions EstStempCens (parameter estimation) and
PredStempCens (prediction in new locations):
library(StempCens)
# Initial parameter values
beta <- c(-1,1.50)
phi <- 5; rho <- 0.60
tau2 <- 0.80; sigma2 <- 2
# Simulating data
n1 <- 17 # Number of spatial locations
n2 <- 5 # Number of temporal index
set.seed(12345)
x.co <- round(runif(n1,0,10),9) # X coordinate
y.co <- round(runif(n1,0,10),9) # Y coordinate
coord <- cbind(x.co,y.co) # Cartesian coordinates without repetitions
coord2 <- cbind(rep(x.co,each=n2),rep(y.co,each=n2)) # Cartesian coordinates with repetitions
time <- as.matrix(seq(1,n2)) # Time index without repetitions
time2 <- as.matrix(rep(time,n1)) # Time index with repetitions
x1 <- rexp(n1*n2,2)
x2 <- rnorm(n1*n2,2,1)
x <- cbind(x1,x2) # Covariates
media <- x%*%beta
# Covariance matrix
Ms <- as.matrix(dist(coord)) # Spatial distances
Mt <- as.matrix(dist(time)) # Temporal distances
Cov <- CovarianceM(phi,rho,tau2,sigma2,Ms,Mt,0.50,"pow.exp")
# Data
require(mvtnorm)
y <- as.vector(rmvnorm(1,mean=as.vector(media),sigma=Cov))
data <- data.frame(coord2,time2,y,x)
names(data) <- c("x.coord","y.coord","time","yObs","x1","x2")
# Splitting the dataset
local.est <- coord[-c(4,13),]
data.est <- data[data$x.coord%in%local.est[,1]&data$y.coord%in%local.est[,2],]
data.valid <- data[data$x.coord%in%coord[c(4,13),1]&data$y.coord%in%coord[c(4,13),2],]
# Censored
perc <- 0.10
y <- data.est$yObs
aa <- sort(y); bb <- aa[1:(perc*nrow(data.est))]; cutof <- bb[perc*nrow(data.est)]
cc <- matrix(1,nrow(data.est),1)*(y<=cutof)
y[cc==1] <- cutof
data.est <- cbind(data.est[,-c(4,5,6)],y,cc,data.est[,c(5,6)])
names(data.est) <- c("x.coord","y.coord","time","yObs","censored","x1","x2")
# Estimation
y <- data.est$yObs
x <- cbind(data.est$x1,data.est$x2)
cc <- data.est$censored
time2 <- matrix(data.est$time)
coord2 <- data.est[,1:2]
LI <- y; LI[cc==1] = -Inf # Left-censored
LS <- y
est_teste <- EstStempCens(y, x, cc, time2, coord2, LI, LS, init.phi=3.5,
init.rho=0.5, init.tau2=1, kappa=0.5, type.S="pow.exp",
IMatrix=TRUE, M=20, perc=0.25, MaxIter=300, pc=0.20)
# Prediction
locPre <- data.valid[,1:2]
timePre <- matrix(data.valid$time)
xPre <- cbind(data.valid$x1,data.valid$x2)
pre_teste <- PredStempCens(est_teste, locPre, timePre, xPre)
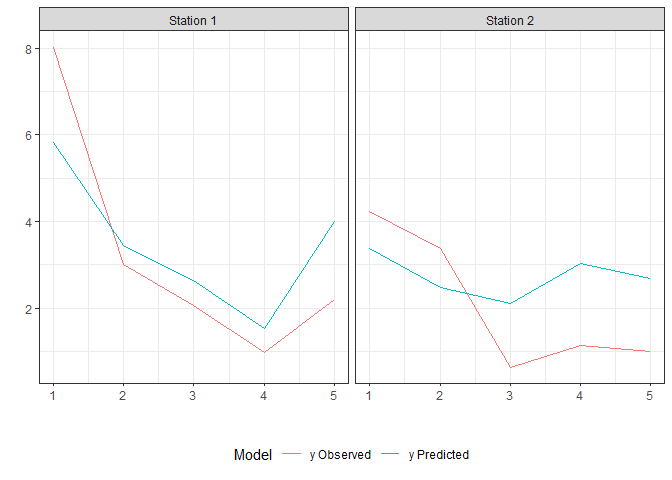
library(ggplot2)
Model <- rep(c("y Observed","y Predicted"),each=10)
station <- rep(rep(c("Station 1", "Station 2"),each=5),times=2)
xcoord1 <- rep(seq(1:5),4)
ycoord1 <- c(data.valid$yObs,pre_teste$predValues)
data2 <- data.frame(Model,station,xcoord1,ycoord1)
ggplot(data=data2,aes(x=xcoord1,y=ycoord1)) + geom_line(aes(color=Model)) +
facet_wrap(station~.,nrow=2) + labs(x="",y="") + theme(legend.position="bottom")For the diagnostic analysis in the EstStempCens function
the parameter input IMatrix needs to be
TRUE.
diag <- DiagStempCens(est, type.diag="location", diag.plot = TRUE, ck=1)Cook, R-Dennis. 1977. “Detection of Influential Observation in Linear Regression.” Technometrics 19 (1): 15–18. https://doi.org/10.1080/00401706.1977.10489493.
Delyon, Bernard, Marc Lavielle, and Eric Moulines. 1999. “Convergence of a Stochastic Approximation Version of the EM Algorithm.” Annals of Statistics 27 (1): 94–128. https://doi.org/10.1214/aos/1018031103.
Louis, Thomas. 1982. “Finding the Observed Information Matrix When Using the Em Algorithm.” Journal of the Royal Statistical Society: Series B (Methodological) 44 (2): 226–33. https://doi.org/10.1111/j.2517-6161.1982.tb01203.x.
Zhu, Hongtu, Sik-Yum Lee, Bo-Cheng Wei, and Julie Zhou. 2001. “Case-Deletion Measures for Models with Incomplete Data.” Biometrika 88 (3): 727–37. https://doi.org/10.1093/biomet/88.3.727.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.