The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
This is the R-package accompanying the paper Convex optimization for the
densest subgraph and densest submatrix problems.
See also Matlab-code
The problem of identifying a dense submatrix is a fundamental problem in the analysis of matrix structure and complex networks. This package provides tools for identifying the densest submatrix of the fixed size in a given graph/matrix using first-order optimization methods.
See the tutorials below to get started.
#Install the development version from GitHub:
# install.packages("remotes")
remotes::install_github("pbombina/admmDensenstSubmatrix")To also build the vignettes use:
#install.packages("remotes")
remotes::install_github("pbombina/admmDensenstSubmatrix", dependencies = TRUE,
build_vignettes = TRUE)This section gives a brief overview of the different functions included in this package. For more details use help(‘function’) or doc(‘function’).
R-package contains the functions: -
plantedsubmatrix.R generates binary matrix sampled from
dense submatrix of particular size - densub.R ADMM
algorithm for our relaxation of the densest subgraph and submatrix
problems - mat_shrink.R soft-threholding operator applied
to vector of singular values (used in X-update step of
densub.R)
We test this package on two different types of data: first, using random matrices sampled from the planted dense m x n submtarix model and, second, real-world collaboration and communication networks.
We first generate a random matrix with noise obscuring the planted
submatrix using the function plantedsubmatrix. and then
call the function densub to recover the planted
submatrix.
# Initialize problem size and densities
# You can play around with these parameters
M <- 100 #number of rows of sampled matrix
N <- 200 #number of columns of sampled matrix
m <- 50 #number of rows of dense submatrix
n <- 40 #number of columns of dense submatrix
p <- 0.25 # noise density
q <- 0.85 #in-group density
#Make binary matrix with mn-submatrix
random<-plantedsubmatrix(M = M, N = N,m = m,n = n,p = p,q = q)After generating the structure random containing the
random matrix with desired planted structure, we can visually represent
the matrix and planted submatrix as two-tone images, where dark pixels
correspond to nonzero entries, and light pixels correspond to zero
entries, using the following commands.
# Plot sampled G and matrix representations.
image(random$sampled_matrix, useRaster = TRUE, axes = FALSE, main = "Matrix A")
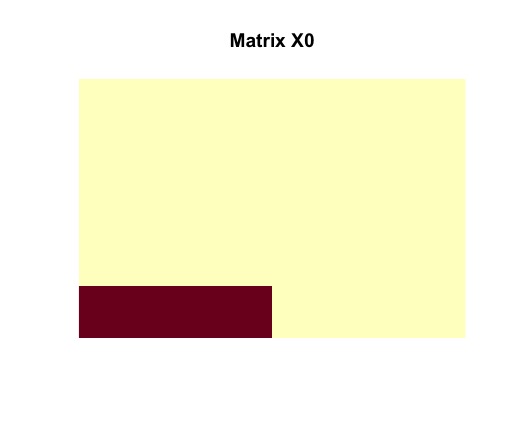
image(random$dense_submatrix, useRaster = TRUE, axes = FALSE, main = "Matrix X0")
image(random$disagreements, useRaster = TRUE, axes = FALSE, main = "Matrix Y0")Tne vizualization of the randomly generated matrix helps us to understand its structure. It is clear that contains a dense block (in the bottom left corner).

We can remove all noise and isolate an image of a rank-one matrix with nonzero entries.
Then we vizualize matrix to see the number of disagreements between original matrix and .

We call the ADMM solver and visualize the output using the following commands.
#Call ADMM solver
admm <- densub(G = random$sampled_matrix, m = m, n = n, tau = 0.35, gamma = 6/(sqrt(m*n)*(q-p)), opt_tol = 1.0e-4,maxiter = 500, quiet = TRUE)
#Plot results
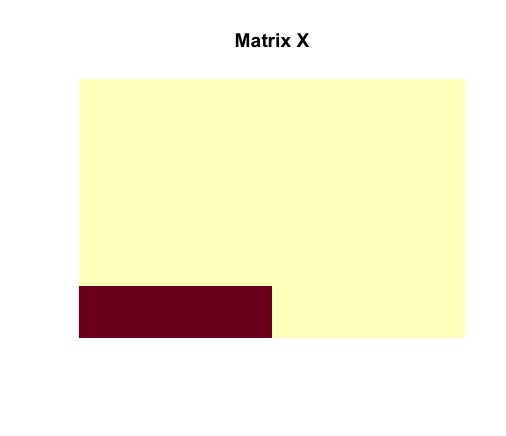
image(admm$X, useRaster = TRUE, axes = FALSE, main = "Matrix X")
image(admm$Y, useRaster = TRUE, axes = FALSE, main = "Matrix Y")
The ADMM solver returns the optimal solutions and . It must be noted that matrices and are identical to the actual structures of and . The planted submatrix is recovered.

The following is a simple example on how one could use the package to analyze the collaboration network found in the JAZZ dataset. It is known that this network contains a cluster of 100 musicians which performed together.

We have already prepared dataset to work with. More details can be
found in the provided file JAZZ_IN_R.R ( in
vignettes folder).
#Load dataset
load(file = "JAZZ.RData")
#Initialize problem size and densities
G <- new #define matrix G equivalent to JAZZ dataset
m <- 100 #clique size or the number of rows of the dense submatrix
n <- 100 #clique size of the number of columns of the dense sumbatrix
tau <- 0.85 #regularization parameter
opt_tol <- 1.0e-2 #optimal tolerance
maxiter <- 2000 #number of iterations
gamma <- 8/n #regularization parameter
#call ADMM solver
admm <- densub(G = G, m = m, n = n, tau = tau, gamma = gamma, opt_tol = opt_tol, maxiter=maxiter, quiet = TRUE)
# Planted solution X0
X0 <- matrix(0L, nrow = 198, ncol = 198) #construct rank-one matrix X0
X0[1:100,1:100] <- matrix(1L, nrow = 100, ncol = 100)#define dense block
# Planted solution Y0
Y0 <- matrix(0L, nrow = 198, ncol = 198) #construct matrix for counting disagreements between G and X0
Y0[1:100,1:100] < matrix(1L,nrow = 100,ncol = 1000)-G[1:100,1:100]
#Check primal and dual residuals
C <- admm$X-X0
a <- norm(C, "F") #Frobenius norm of matrix C
b <- norm(X0,"F") #Frobenius norm of matrix X0
recovery <- matrix(0L,nrow = 1, ncol = 1)#create recovery condition matrix
if (a/b^2<opt_tol){ #Recovery condition
recovery = recovery+1
} else {
recovery = 0
}Our algorithm converges to the dense submatrix representing the community of 100 musicians after 50 iterations.
If you encounter a clear bug, please file a minimal reproducible example on github.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.