
The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

An R package containing commonly used functions for analyzing behavioral economic discounting data.
The package supports scoring of the 27-Item Monetary Choice Questionnaire (see Kaplan et al., 2016), calculating k values (and Area Under the Curve metrics) from indifference points using nonlinear regression (Mazur’s simple hyperbola and exponential), and scoring of the minute discounting task (see Koffarnus & Bickel, 2014) using the Qualtrics 5-trial discounting template (see the Qualtrics Minute Discounting User Guide), which is also available as a .qsf file in this package.
Currently, this version (0.3.2) appears stable. I encourage you to use it but be aware that, as with any software release, there might be (unknown) bugs present. I’ve tried hard to make this version usable while including the core functionality (described more below). However, if you find issues or would like to contribute, please open an issue on my GitHub page or email me.
You may also use these functions in the Shinybeez web application and also found at the GitHub page.
If you use this package in your own work, please consider citing the package:
Kaplan, B. A. (2023). beezdiscounting: Behavioral Economic Easy Discounting. R package version 0.3.1, https://github.com/brentkaplan/beezdiscounting
You can also find the latest citation using
citation("beezdemand")
The latest stable version of beezdiscounting (currently
v.0.3.1) can be found on CRAN and
installed using the following command. The first time you install the
package, you may be asked to select a CRAN mirror. Simply select the
mirror geographically closest to you.
install.packages("beezdiscounting")
library(beezdiscounting)To install a stable release directly from GitHub, first
install and load the devtools package. Then, use
install_github to install the package and associated
vignette. You don’t need to download anything directly from GitHub, as you
should use the following instructions:
install.packages("devtools")
devtools::install_github("brentkaplan/beezdiscounting")
library(beezdiscounting)An example dataset of responses on the 27-Item Monetary Choice
Questionnaire is provided. This object is called mcq27 and
is located within the beezdiscounting package. These data
are the example data used in the paper by Kaplan et al,
2016. Note the format of the data, which is called “long format”.
Long format data are data structured such that repeated observations are
stacked in multiple rows, rather than across columns.
| subjectid | questionid | response | |
|---|---|---|---|
| 1 | 1 | 1 | 0 |
| 2 | 1 | 2 | 0 |
| 3 | 1 | 3 | 0 |
| 4 | 1 | 4 | 1 |
| 5 | 1 | 5 | 1 |
| 6 | 1 | 6 | 0 |
| 7 | 1 | 7 | 1 |
| 28 | 2 | 1 | 0 |
| 29 | 2 | 2 | 1 |
| 30 | 2 | 3 | 1 |
| 31 | 2 | 4 | 1 |
| 32 | 2 | 5 | 1 |
| 33 | 2 | 6 | 0 |
| 34 | 2 | 7 | 1 |
The first column contains the subject id. The second column contains the question id. The third column contains the response (0 for smaller sooner, 1 for larger later)
beezdiscounting includes several helper functions to
reshape data.
long_to_wide_mcq()Long format data are widened such that subject id is the first column and each subsequent column contains the response associated with the question (specified as column names).
wide <- long_to_wide_mcq(generate_data_mcq(2))
knitr::kable(wide[, c(1:5, 24:28)], caption = "Wide Format Data")| subjectid | 1 | 2 | 3 | 4 | 23 | 24 | 25 | 26 | 27 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 |
| 2 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 |
Wide Format Data
wide_to_long_mcq()Wide data (see example of wide data above) are made long such that subject id is in the first column, question id (inferred from the column names from the wide format dataframe) is the second column, and the response is the third column.
long <- wide_to_long_mcq(wide, items = 27)
knitr::kable(long[c(1:5, 28:32), ], caption = "Long Format Data")| subjectid | questionid | response |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 1 | 5 | 0 |
| 2 | 1 | 1 |
| 2 | 2 | 1 |
| 2 | 3 | 1 |
| 2 | 4 | 0 |
| 2 | 5 | 1 |
Long Format Data
wide_to_long_mcq_excel()A different ‘type’ of wide data is that used in the 27-Item Monetary
Choice Questionnaire Automated Excel Scorer (Kaplan et al,
2016). In this format, the first column is the question id and each
subsequent column represents a subject (as the column name) and the
response in rows (see the example below). This function takes the data
from that format and converts it to the format needed for
beezdiscounting functions.
knitr::kable(wide_excel[c(1:5, 22:27), ],
caption = "Format Expected in the 27-Item MCQ Excel Scorer")| questionid | 1 | 2 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 1 |
| 4 | 1 | 0 |
| 5 | 0 | 1 |
| 22 | 1 | 0 |
| 23 | 1 | 1 |
| 24 | 1 | 1 |
| 25 | 1 | 1 |
| 26 | 1 | 1 |
| 27 | 0 | 1 |
Format Expected in the 27-Item MCQ Excel Scorer
long_excel <- wide_to_long_mcq_excel(wide_excel)
knitr::kable(long_excel[c(1:5, 28:32), ], caption = "Long Format")| subjectid | questionid | response |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 1 | 5 | 0 |
| 2 | 1 | 1 |
| 2 | 2 | 1 |
| 2 | 3 | 1 |
| 2 | 4 | 0 |
| 2 | 5 | 1 |
Long Format
long_to_wide_mcq_excel()Data can be manipulated from long form into a form used by the 27-Item Monetary Choice Questionnaire Automated Excel Scorer.
wide_excel <- long_to_wide_mcq_excel(long_excel)
knitr::kable(wide_excel[c(1:5, 22:27), ],
caption = "Format Expected in the 27-Item MCQ Excel Scorer")| questionid | 1 | 2 |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 1 | 1 |
| 3 | 1 | 1 |
| 4 | 1 | 0 |
| 5 | 0 | 1 |
| 22 | 1 | 0 |
| 23 | 1 | 1 |
| 24 | 1 | 1 |
| 25 | 1 | 1 |
| 26 | 1 | 1 |
| 27 | 0 | 1 |
Format Expected in the 27-Item MCQ Excel Scorer
Generate data specifying reproducibility and proportion of
NA responses.
## fake data with no missing values
fake_data_no_missing <- generate_data_mcq(n_ids = 2, n_items = 27,
seed = 1234, prop_na = 0)
knitr::kable(fake_data_no_missing, caption = "Fake Data - No Missings")| subjectid | questionid | response |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 1 |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 1 | 5 | 0 |
| 1 | 6 | 1 |
| 1 | 7 | 0 |
| 1 | 8 | 0 |
| 1 | 9 | 0 |
| 1 | 10 | 1 |
| 1 | 11 | 1 |
| 1 | 12 | 1 |
| 1 | 13 | 1 |
| 1 | 14 | 0 |
| 1 | 15 | 1 |
| 1 | 16 | 1 |
| 1 | 17 | 1 |
| 1 | 18 | 0 |
| 1 | 19 | 1 |
| 1 | 20 | 1 |
| 1 | 21 | 1 |
| 1 | 22 | 1 |
| 1 | 23 | 1 |
| 1 | 24 | 1 |
| 1 | 25 | 1 |
| 1 | 26 | 1 |
| 1 | 27 | 0 |
| 2 | 1 | 1 |
| 2 | 2 | 1 |
| 2 | 3 | 1 |
| 2 | 4 | 0 |
| 2 | 5 | 1 |
| 2 | 6 | 0 |
| 2 | 7 | 0 |
| 2 | 8 | 0 |
| 2 | 9 | 1 |
| 2 | 10 | 0 |
| 2 | 11 | 1 |
| 2 | 12 | 1 |
| 2 | 13 | 0 |
| 2 | 14 | 1 |
| 2 | 15 | 0 |
| 2 | 16 | 1 |
| 2 | 17 | 1 |
| 2 | 18 | 1 |
| 2 | 19 | 0 |
| 2 | 20 | 0 |
| 2 | 21 | 0 |
| 2 | 22 | 0 |
| 2 | 23 | 1 |
| 2 | 24 | 1 |
| 2 | 25 | 1 |
| 2 | 26 | 1 |
| 2 | 27 | 1 |
Fake Data - No Missings
## fake data with missing values
fake_data_missing <- generate_data_mcq(n_ids = 2, n_items = 27,
seed = 1234, prop_na = .1)
knitr::kable(fake_data_missing, caption = "Fake Data - Missings")| subjectid | questionid | response |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | NA |
| 1 | 3 | 1 |
| 1 | 4 | 1 |
| 1 | 5 | 0 |
| 1 | 6 | 1 |
| 1 | 7 | 0 |
| 1 | 8 | 0 |
| 1 | 9 | 0 |
| 1 | 10 | 1 |
| 1 | 11 | 1 |
| 1 | 12 | 1 |
| 1 | 13 | 1 |
| 1 | 14 | 0 |
| 1 | 15 | NA |
| 1 | 16 | 1 |
| 1 | 17 | 1 |
| 1 | 18 | 0 |
| 1 | 19 | 1 |
| 1 | 20 | 1 |
| 1 | 21 | 1 |
| 1 | 22 | 1 |
| 1 | 23 | 1 |
| 1 | 24 | 1 |
| 1 | 25 | 1 |
| 1 | 26 | 1 |
| 1 | 27 | 0 |
| 2 | 1 | 1 |
| 2 | 2 | 1 |
| 2 | 3 | 1 |
| 2 | 4 | 0 |
| 2 | 5 | 1 |
| 2 | 6 | 0 |
| 2 | 7 | 0 |
| 2 | 8 | 0 |
| 2 | 9 | 1 |
| 2 | 10 | 0 |
| 2 | 11 | NA |
| 2 | 12 | 1 |
| 2 | 13 | 0 |
| 2 | 14 | 1 |
| 2 | 15 | 0 |
| 2 | 16 | NA |
| 2 | 17 | 1 |
| 2 | 18 | 1 |
| 2 | 19 | 0 |
| 2 | 20 | 0 |
| 2 | 21 | 0 |
| 2 | 22 | NA |
| 2 | 23 | 1 |
| 2 | 24 | 1 |
| 2 | 25 | 1 |
| 2 | 26 | 1 |
| 2 | 27 | 1 |
Fake Data - Missings
MCQ data can be scored regularly and can also impute using various methods specified by Yeh et al, 2023
## normal scoring of data with no missing values
tbl1 <- score_mcq27(fake_data_no_missing)| subjectid | overall_k | small_k | medium_k | large_k | geomean_k |
|---|---|---|---|---|---|
| 1 | 0.000158 | 0.000158 | 0.000158 | 0.000251 | 0.000185 |
| 2 | 0.000251 | 0.001562 | 0.004469 | 0.000158 | 0.001034 |
k Values
| subjectid | overall_consistency | small_consistency | medium_consistency | large_consistency | composite_consistency |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 1.000000 | 0.777778 |
| 2 | 0.629630 | 0.777778 | 0.555556 | 0.666667 | 0.666667 |
Consistency Scores
| subjectid | overall_proportion | small_proportion | medium_proportion | large_proportion | impute_method |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 0.888889 | none |
| 2 | 0.592593 | 0.555556 | 0.555556 | 0.666667 | none |
Proportions
## normal scoring of data with missings with no imputation
tbl2 <- score_mcq27(fake_data_missing)| subjectid | overall_k | small_k | medium_k | large_k | geomean_k |
|---|---|---|---|---|---|
| 1 | NA | 0.000158 | 0.000158 | NA | NA |
| 2 | NA | NA | NA | 0.000158 | NA |
k Values
| subjectid | overall_consistency | small_consistency | medium_consistency | large_consistency | composite_consistency |
|---|---|---|---|---|---|
| 1 | NA | 0.666667 | 0.666667 | NA | NA |
| 2 | NA | NA | NA | 0.666667 | NA |
Consistency Scores
| subjectid | overall_proportion | small_proportion | medium_proportion | large_proportion | impute_method |
|---|---|---|---|---|---|
| 1 | NA | 0.666667 | 0.666667 | NA | none |
| 2 | NA | NA | NA | 0.666667 | none |
Proportions
This approach (Group Geometric Mean) “…calculates the composite k when at least one of the three amount set ks is fully available” (Yeh et al, 2023)
tbl3 <- score_mcq27(fake_data_missing, impute_method = "GGM")| subjectid | overall_k | small_k | medium_k | large_k | geomean_k |
|---|---|---|---|---|---|
| 1 | NA | 0.000158 | 0.000158 | NA | 0.000158 |
| 2 | NA | NA | NA | 0.000158 | 0.000158 |
k Values
| subjectid | overall_consistency | small_consistency | medium_consistency | large_consistency | composite_consistency |
|---|---|---|---|---|---|
| 1 | NA | 0.666667 | 0.666667 | NA | NA |
| 2 | NA | NA | NA | 0.666667 | NA |
Consistency Scores
| subjectid | overall_proportion | small_proportion | medium_proportion | large_proportion | impute_method |
|---|---|---|---|---|---|
| 1 | NA | 0.666667 | 0.666667 | NA | GGM |
| 2 | NA | NA | NA | 0.666667 | GGM |
Proportions
This approach (Item Nearest Neighbor) “…replaces the missing value with the congruent non-missing responses to the items corresponding to the same k value” (Yeh et al, 2023)
tbl4 <- score_mcq27(fake_data_missing, impute_method = "INN")| subjectid | overall_k | small_k | medium_k | large_k | geomean_k |
|---|---|---|---|---|---|
| 1 | 0.000158 | 0.000158 | 0.000158 | 0.000251 | 0.000185 |
| 2 | NA | NA | 0.063154 | 0.000158 | NA |
k Values
| subjectid | overall_consistency | small_consistency | medium_consistency | large_consistency | composite_consistency |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 1.000000 | 0.777778 |
| 2 | NA | NA | 0.666667 | 0.666667 | NA |
Consistency Scores
| subjectid | overall_proportion | small_proportion | medium_proportion | large_proportion | impute_method |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 0.888889 | INN |
| 2 | NA | NA | 0.444444 | 0.666667 | INN |
Proportions
This approach (Item Nearest Neighbor with Random) “… is identical to [INN no random component], except that when a missing response cannot be resolved, this datum will be randomly replaced with 0 or 1, corresponding to choosing immediate or delayed rewards, respectively” (Yeh et al, 2023)
tbl5 <- score_mcq27(fake_data_missing, impute_method = "INN",
random = TRUE)| subjectid | overall_k | small_k | medium_k | large_k | geomean_k |
|---|---|---|---|---|---|
| 1 | 0.000158 | 0.000158 | 0.000158 | 0.000251 | 0.000185 |
| 2 | 0.000251 | 0.001562 | 0.063154 | 0.000158 | 0.002500 |
k Values
| subjectid | overall_consistency | small_consistency | medium_consistency | large_consistency | composite_consistency |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 1.000000 | 0.777778 |
| 2 | 0.592593 | 0.777778 | 0.666667 | 0.666667 | 0.703704 |
Consistency Scores
| subjectid | overall_proportion | small_proportion | medium_proportion | large_proportion | impute_method |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 0.888889 | INN with random |
| 2 | 0.555556 | 0.555556 | 0.444444 | 0.666667 | INN with random |
Proportions
You can also return a list when INN imputation with random is
specified. This is helpful to see what values replaced the missings
(NAs) in the original dataset.
lst <- score_mcq27(fake_data_missing, impute_method = "INN",
random = TRUE, return_data = TRUE)The scoring summary metric dataframe as before (access via
...$results):
| subjectid | overall_k | small_k | medium_k | large_k | geomean_k |
|---|---|---|---|---|---|
| 1 | 0.000158 | 0.000158 | 0.000158 | 0.000251 | 0.000185 |
| 2 | 0.000251 | 0.001562 | 0.063154 | 0.000158 | 0.002500 |
k Values
| subjectid | overall_consistency | small_consistency | medium_consistency | large_consistency | composite_consistency |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 1.000000 | 0.777778 |
| 2 | 0.555556 | 0.666667 | 0.666667 | 0.666667 | 0.666667 |
Consistency Scores
| subjectid | overall_proportion | small_proportion | medium_proportion | large_proportion | impute_method |
|---|---|---|---|---|---|
| 1 | 0.740741 | 0.666667 | 0.666667 | 0.888889 | INN with random |
| 2 | 0.518519 | 0.444444 | 0.444444 | 0.666667 | INN with random |
Proportions
The original data and the new responses imputed (access via
...$data):
| subjectid | questionid | response | newresponse |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 1 | 2 | NA | 1 |
| 1 | 3 | 1 | 1 |
| 1 | 4 | 1 | 1 |
| 1 | 5 | 0 | 0 |
| 1 | 6 | 1 | 1 |
| 1 | 7 | 0 | 0 |
| 1 | 8 | 0 | 0 |
| 1 | 9 | 0 | 0 |
| 1 | 10 | 1 | 1 |
| 1 | 11 | 1 | 1 |
| 1 | 12 | 1 | 1 |
| 1 | 13 | 1 | 1 |
| 1 | 14 | 0 | 0 |
| 1 | 15 | NA | 1 |
| 1 | 16 | 1 | 1 |
| 1 | 17 | 1 | 1 |
| 1 | 18 | 0 | 0 |
| 1 | 19 | 1 | 1 |
| 1 | 20 | 1 | 1 |
| 1 | 21 | 1 | 1 |
| 1 | 22 | 1 | 1 |
| 1 | 23 | 1 | 1 |
| 1 | 24 | 1 | 1 |
| 1 | 25 | 1 | 1 |
| 1 | 26 | 1 | 1 |
| 1 | 27 | 0 | 0 |
| 2 | 1 | 1 | 1 |
| 2 | 2 | 1 | 1 |
| 2 | 3 | 1 | 1 |
| 2 | 4 | 0 | 0 |
| 2 | 5 | 1 | 1 |
| 2 | 6 | 0 | 0 |
| 2 | 7 | 0 | 0 |
| 2 | 8 | 0 | 0 |
| 2 | 9 | 1 | 1 |
| 2 | 10 | 0 | 0 |
| 2 | 11 | NA | 0 |
| 2 | 12 | 1 | 1 |
| 2 | 13 | 0 | 0 |
| 2 | 14 | 1 | 1 |
| 2 | 15 | 0 | 0 |
| 2 | 16 | NA | 0 |
| 2 | 17 | 1 | 1 |
| 2 | 18 | 1 | 1 |
| 2 | 19 | 0 | 0 |
| 2 | 20 | 0 | 0 |
| 2 | 21 | 0 | 0 |
| 2 | 22 | NA | 0 |
| 2 | 23 | 1 | 1 |
| 2 | 24 | 1 | 1 |
| 2 | 25 | 1 | 1 |
| 2 | 26 | 1 | 1 |
| 2 | 27 | 1 | 1 |
Original Data and Imputed Data
The data must be in a dataframe with the following columns: -
id: participant ID - x: delay -
y: indifference point
For example, the following data set is available in the package:
dd_ip
knitr::kable(dd_ip[1:12, ], caption = "Indifference Point Data")| id | x | y |
|---|---|---|
| P1 | 1 | 0.8162505 |
| P1 | 7 | 0.3908523 |
| P1 | 30 | 0.0191631 |
| P1 | 90 | 0.0990859 |
| P1 | 180 | 0.0134581 |
| P1 | 365 | 0.0035518 |
| P2 | 1 | 0.5724503 |
| P2 | 7 | 0.1652014 |
| P2 | 30 | 0.0326867 |
| P2 | 90 | 0.0802244 |
| P2 | 180 | 0.0275921 |
| P2 | 365 | 0.0247967 |
Indifference Point Data
The check_unsystematic() function can be used to check
whether the data conform to the assumptions of the Johnson & Bickel
(2008) method. The function is designed to work with a single
participant. As will often be the case, you will want to run this for
each unique participant in the dataset as shown below:
unsys <- dd_ip |>
dplyr::group_split(id) |>
purrr::map_dfr(~ check_unsystematic(
dat = .x,
ll = 1, # LL specification
c1 = 0.2, # Criterion 1 threshold
c2 = 0.1 # Criterion 2 threshold
)) |>
dplyr::mutate(id = factor(id, levels = unique(dd_ip$id))) |>
dplyr::arrange(id) |>
dplyr::slice(1:5)
knitr::kable(unsys, caption = "Unsystematic Data Output")| id | c1_pass | c2_pass |
|---|---|---|
| P1 | TRUE | TRUE |
| P2 | TRUE | TRUE |
| P3 | TRUE | TRUE |
| P4 | TRUE | TRUE |
| P5 | TRUE | TRUE |
Unsystematic Data Output
The fit_dd() function can be used to estimate k
values from either the simple hyperbola (Mazur, 1987) or exponential
equation. The output of this function can then be used in
results_dd() and plot_dd() to obtain a table
of results and plots of data.
First use the fit_dd() function to fit the data:
dd_fit <- fit_dd(
dat = dd_ip,
equation = "Hyperbolic",
method = "Two Stage"
)Then use the results_dd() function to get a table of
results. The results table automatically includes measures of Area Under
the Curve (AUC). Three different AUC measures are calculated:
auc_regular: AUC calculated using the regular
trapezoidal rule
auc_log10: AUC calculated using the trapezoidal rule
on the log10-transformed x values (Borges et al., 2016)
auc_ord: AUC calculated using the trapezoidal rule
on the ordinally transformed x values (Borges et al., 2016)
dd_results <- results_dd(dd_fit) |>
dplyr::mutate(id = factor(id, levels = unique(dd_ip$id))) |>
dplyr::arrange(id) |>
dplyr::slice(1:5)
knitr::kable(dd_results[, c(1:7, 21:22)], caption = "Parameter Estimates and Information")| method | id | term | estimate | std.error | statistic | p.value | conf_low | conf_high |
|---|---|---|---|---|---|---|---|---|
| Two Stage | P1 | k | 0.2481617 | 0.0432495 | 5.737907 | 0.0022525 | 0.1369853 | 0.3593381 |
| Two Stage | P2 | k | 0.7338717 | 0.0839848 | 8.738149 | 0.0003252 | 0.5179819 | 0.9497615 |
| Two Stage | P3 | k | 0.5551845 | 0.0810197 | 6.852465 | 0.0010110 | 0.3469168 | 0.7634522 |
| Two Stage | P4 | k | 0.2844655 | 0.0264744 | 10.744931 | 0.0001210 | 0.2164109 | 0.3525200 |
| Two Stage | P5 | k | 1.0135883 | 0.0760710 | 13.324235 | 0.0000426 | 0.8180415 | 1.2091351 |
Parameter Estimates and Information
knitr::kable(dd_results[, c(1:3, 8:17)], caption = "Model Information")| method | id | term | sigma | isConv | finTol | logLik | AIC | BIC | deviance | df.residual | nobs | R2 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Two Stage | P1 | k | 0.0529456 | TRUE | 0 | 9.664278 | -15.32856 | -15.74504 | 0.0140162 | 5 | 6 | 0.9735088 |
| Two Stage | P2 | k | 0.0324102 | TRUE | 0 | 12.609020 | -21.21804 | -21.63452 | 0.0052521 | 5 | 6 | 0.9769628 |
| Two Stage | P3 | k | 0.0419241 | TRUE | 0 | 11.064704 | -18.12941 | -18.54589 | 0.0087881 | 5 | 6 | 0.9715690 |
| Two Stage | P4 | k | 0.0278923 | TRUE | 0 | 13.509754 | -23.01951 | -23.43599 | 0.0038899 | 5 | 6 | 0.9917668 |
| Two Stage | P5 | k | 0.0205973 | TRUE | 0 | 15.328915 | -26.65783 | -27.07431 | 0.0021212 | 5 | 6 | 0.9886979 |
Model Information
knitr::kable(dd_results[, c(1:2, 18:20)], caption = "Area Under the Curve Values")| method | id | auc_regular | auc_log10 | auc_ord |
|---|---|---|---|---|
| Two Stage | P1 | 0.0508842 | 0.2347151 | 0.1864921 |
| Two Stage | P2 | 0.0482794 | 0.1462015 | 0.1208656 |
| Two Stage | P3 | 0.0409701 | 0.1685302 | 0.1352153 |
| Two Stage | P4 | 0.0313241 | 0.2169982 | 0.1664288 |
| Two Stage | P5 | 0.0169814 | 0.1126664 | 0.0867586 |
Area Under the Curve Values
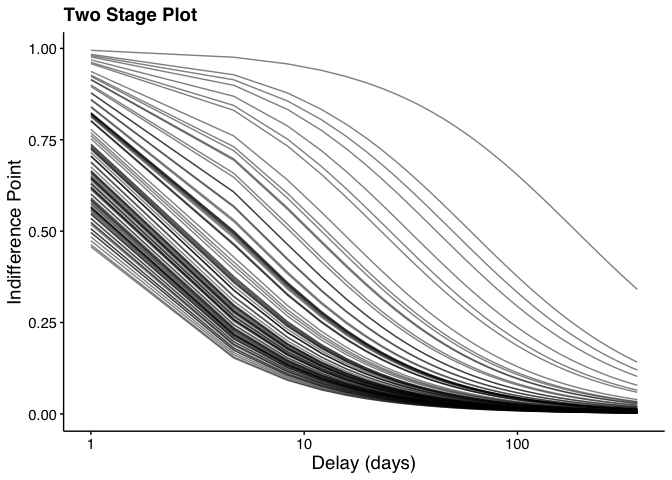
Finally, use the plot_dd() function to plot the
data:
plot_dd(
fit_dd_object = dd_fit,
xlabel = "Delay (days)", # Specify x label
ylabel = "Indifference Point", # Specify y label
title = "Two Stage Plot", # Specify plot title
logx = TRUE # Specify log scale for x axis
)
dd_out <- calc_dd(five.fivetrial_dd)
knitr::kable(dd_out, caption = "Scoring Summary of the 5.5 Trial Delay Discounting Task")| ResponseId | index | q | firstclick | lastclick | pagesubmit | totalclicks | response | attentionflag | kval | ed50 |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | I16 | 1 | 1.761 | 1.761 | 3.337 | 1 | ll | No | 0.0067058 | 149.1249275 |
| 1 | I24 | 2 | 7.729 | 7.729 | 8.457 | 1 | ss | No | 0.0067058 | 149.1249275 |
| 1 | I20 | 3 | 1.558 | 1.558 | 3.377 | 1 | ll | No | 0.0067058 | 149.1249275 |
| 1 | I22 | 4 | 2.333 | 3.949 | 4.501 | 2 | ss | No | 0.0067058 | 149.1249275 |
| 1 | I21 | 5 | 3.161 | 3.161 | 3.728 | 1 | ss | No | 0.0067058 | 149.1249275 |
| 2 | I16 | 1 | 3.779 | 3.779 | 4.351 | 1 | ss | No | 4.8989795 | 0.2041241 |
| 2 | I8 | 2 | 1.454 | 1.454 | 3.190 | 1 | ss | No | 4.8989795 | 0.2041241 |
| 2 | I4 | 3 | 1.179 | 1.179 | 3.144 | 1 | ll | No | 4.8989795 | 0.2041241 |
| 2 | I6 | 4 | 0.873 | 0.873 | 3.256 | 1 | ss | No | 4.8989795 | 0.2041241 |
| 2 | I5 | 5 | 2.621 | 2.621 | 3.258 | 1 | ss | No | 4.8989795 | 0.2041241 |
| 3 | I16 | 1 | 1.115 | 1.115 | 3.272 | 1 | ss | Yes | NA | NA |
| 3 | I8 | 2 | 0.679 | 0.679 | 3.074 | 1 | ss | Yes | NA | NA |
| 3 | I4 | 3 | 0.606 | 0.606 | 3.044 | 1 | ss | Yes | NA | NA |
| 3 | I2 | 4 | 0.745 | 0.745 | 3.302 | 1 | ss | Yes | NA | NA |
| 3 | I1 | 5 | 0.924 | 0.924 | 4.181 | 1 | ss | Yes | NA | NA |
| 3 | AttendSS | 6 | 1.450 | 1.450 | 4.181 | 1 | ss | Yes | NA | NA |
| 4 | I16 | 1 | 1.011 | 1.011 | 3.190 | 1 | ll | Yes | NA | NA |
| 4 | I24 | 2 | 1.041 | 1.041 | 3.109 | 1 | ll | Yes | NA | NA |
| 4 | I28 | 3 | 0.806 | 0.806 | 3.113 | 1 | ll | Yes | NA | NA |
| 4 | I30 | 4 | 0.822 | 0.822 | 3.487 | 1 | ll | Yes | NA | NA |
| 4 | I31 | 5 | 0.914 | 0.914 | 3.170 | 1 | ll | Yes | NA | NA |
| 4 | AttendLL | 6 | 2.158 | 2.158 | 3.573 | 1 | ll | Yes | NA | NA |
Scoring Summary of the 5.5 Trial Delay Discounting Task
pd_out <- calc_pd(five.fivetrial_pd)
knitr::kable(pd_out, caption = "Scoring Summary of the 5.5 Trial Probability Discounting Task")| ResponseId | index | q | firstclick | lastclick | pagesubmit | totalclicks | response | attentionflag | hval | etheta50 | ep50 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | I16 | 1 | 3.980 | 3.980 | 5.184 | 1 | sc | No | 7.435436 | 0.1344911 | 88.14525 |
| 1 | I8 | 2 | 4.010 | 4.010 | 4.763 | 1 | lu | No | 7.435436 | 0.1344911 | 88.14525 |
| 1 | I12 | 3 | 2.061 | 2.061 | 3.252 | 1 | sc | No | 7.435436 | 0.1344911 | 88.14525 |
| 1 | I10 | 4 | 1.525 | 1.525 | 3.019 | 1 | sc | No | 7.435436 | 0.1344911 | 88.14525 |
| 1 | I9 | 5 | 2.253 | 2.954 | 3.738 | 2 | lu | No | 7.435436 | 0.1344911 | 88.14525 |
| 2 | I16 | 1 | 2.873 | 2.873 | 3.883 | 1 | sc | No | 99.000000 | 0.0101010 | 99.00000 |
| 2 | I8 | 2 | 3.745 | 3.745 | 4.864 | 1 | sc | No | 99.000000 | 0.0101010 | 99.00000 |
| 2 | I4 | 3 | 1.159 | 1.159 | 6.356 | 1 | sc | No | 99.000000 | 0.0101010 | 99.00000 |
| 2 | I2 | 4 | 3.064 | 3.064 | 5.408 | 1 | sc | No | 99.000000 | 0.0101010 | 99.00000 |
| 2 | I1 | 5 | 2.049 | 2.049 | 5.097 | 1 | sc | No | 99.000000 | 0.0101010 | 99.00000 |
| 2 | AttendSS | 6 | 2.295 | 2.295 | 4.641 | 1 | lu | No | 99.000000 | 0.0101010 | 99.00000 |
| 3 | I16 | 1 | 8.933 | 8.933 | 9.769 | 1 | sc | No | 1.601445 | 0.6244361 | 61.55983 |
| 3 | I8 | 2 | 2.163 | 2.163 | 2.981 | 1 | lu | No | 1.601445 | 0.6244361 | 61.55983 |
| 3 | I12 | 3 | 3.129 | 3.129 | 3.895 | 1 | lu | No | 1.601445 | 0.6244361 | 61.55983 |
| 3 | I14 | 4 | 2.655 | 2.655 | 4.855 | 1 | lu | No | 1.601445 | 0.6244361 | 61.55983 |
| 3 | I15 | 5 | 4.021 | 4.021 | 4.705 | 1 | sc | No | 1.601445 | 0.6244361 | 61.55983 |
| 4 | I16 | 1 | 4.415 | 4.415 | 5.382 | 1 | sc | No | 7.435436 | 0.1344911 | 88.14525 |
| 4 | I8 | 2 | 6.123 | 6.123 | 6.974 | 1 | lu | No | 7.435436 | 0.1344911 | 88.14525 |
| 4 | I12 | 3 | 1.673 | 1.673 | 3.191 | 1 | sc | No | 7.435436 | 0.1344911 | 88.14525 |
| 4 | I10 | 4 | 1.757 | 1.757 | 3.259 | 1 | sc | No | 7.435436 | 0.1344911 | 88.14525 |
| 4 | I9 | 5 | 1.207 | 1.207 | 4.592 | 1 | lu | No | 7.435436 | 0.1344911 | 88.14525 |
Scoring Summary of the 5.5 Trial Probability Discounting Task
To learn more about a function and what arguments it takes, type “?” in front of the function name.
?score_mcq27Kaplan, B. A., Amlung, M., Reed, D. D., Jarmolowicz, D. P., McKerchar, T. L., & Lemley, S. M. (2016). Automating scoring of delay discounting for the 21-and 27-item monetary choice questionnaires. The Behavior Analyst, 39, 293-304. https://doi.org/10.1007/s40614-016-0070-9
Reed, D. D., Niileksela, C. R., & Kaplan, B. A. (2013). Behavioral economics: A tutorial for behavior analysts in practice. Behavior Analysis in Practice, 6 (1), 34–54. https://doi.org/10.1007/BF03391790
Mazur, J. E. (1987). An adjusting procedure for studying delayed reinforcement. In M. L. Commons, J. E. Mazur, J. A. Nevin, & H. Rachlin (Eds.), The effect of delay and of intervening events on reinforcement value (pp. 55–73). Lawrence Erlbaum Associates, Inc.
Borges, A. M., Kuang, J., Milhorn, H. and Yi, R. (2016), An alternative approach to calculating Area-Under-the-Curve (AUC) in delay discounting research. Journal of the Experimental Analysis of Behavior, 106, 145-155. https://doi.org/10.1002/jeab.219
Kirby, K. N., Petry, N. M., & Bickel, W. K. (1999). Heroin addicts have higher discount rates for delayed rewards than non-drug-using controls. Journal of Experimental Psychology: General, 128 (1), 78-87. https://doi.org/10.1037//0096-3445.128.1.78
Yeh, Y. H., Tegge, A. N., Freitas-Lemos, R., Myerson, J., Green, L., & Bickel, W. K. (2023). Discounting of delayed rewards: Missing data imputation for the 21-and 27-item monetary choice questionnaires. PLOS ONE, 18 (10), e0292258. https://doi.org/10.1371/journal.pone.0292258
Koffarnus, M. N., & Bickel, W. K. (2014). A 5-trial adjusting delay discounting task: accurate discount rates in less than one minute. Experimental and Clinical Psychopharmacology, 22(3), 222-228. https://doi.org/10.1037/a0035973
Koffarnus, M. N., Rzeszutek, M. J., & Kaplan, B. A. (2021). Additional discounting rates in less than one minute: Task variants for probability and a wider range of delays. https://doi.org/10.13140/RG.2.2.31281.92000
Koffarnus, M. N., Kaplan, B. A., & Stein, J. S. (2017). User guide for Qualtrics minute discounting template. https://doi.org/10.13140/RG.2.2.26495.79527
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.