The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
2022-10-25
The purpose of the cxhull package is to compute the
convex hull of a set of points in arbitrary dimension. Its main function
is named cxhull.
The output of the cxhull function is a list with the
following fields.
vertices: The vertices of the convex hull. Each
vertex is given with its neighbour vertices, its neighbour ridges and
its neighbour facets.
edges: The edges of the convex hull, given as pairs
of vertices identifiers.
ridges: The ridges of the convex hull, i.e. the
elements of the convex hull of dimension dim-2. Thus the
ridges are just the vertices in dimension 2, and they are the edges in
dimension 3.
facets: The facets of the convex hull, i.e. the
elements of the convex hull of dimension dim-1. Thus the
facets are the edges in dimension 2, and they are the faces of the
convex polyhedron in dimension 3.
volume: The volume of the convex hull (area in
dimension 2, volume in dimension 3, hypervolume in higher
dimension).
Let’s look at an example. The points we take are the vertices of a cube and the center of this cube (in the first row):
library(cxhull)
points <- rbind(
c(0.5, 0.5, 0.5),
c(0, 0, 0),
c(0, 0, 1),
c(0, 1, 0),
c(0, 1, 1),
c(1, 0, 0),
c(1, 0, 1),
c(1, 1, 0),
c(1, 1, 1)
)
hull <- cxhull(points)Obviously, the convex hull of these points is the cube. We can quickly see that the convex hull has 8 vertices, 12 edges, 12 ridges, 6 facets, and its volume is 1:
str(hull, max = 1)
## List of 5
## $ vertices:List of 8
## $ edges : int [1:12, 1:2] 2 2 2 3 3 4 4 5 6 6 ...
## $ ridges :List of 12
## $ facets :List of 6
## $ volume : num 1
## - attr(*, "3d")= logi TRUEEach vertex, each ridge, and each facet has an identifier. A vertex
identifier is the index of the row corresponding to this vertex in the
set of points passed to the cxhull function. It is given in
the field id of the vertex:
hull[["vertices"]][[1]]
## $id
## [1] 2
##
## $point
## [1] 0 0 0
##
## $neighvertices
## [1] 3 4 6
##
## $neighridges
## [1] 1 2 5
##
## $neighfacets
## [1] 1 2 4Also, the list of vertices is named with the identifiers:
names(hull[["vertices"]])
## [1] "2" "3" "4" "5" "6" "7" "8" "9"Edges are given as a matrix, each row representing an edge given as a pair of vertices identifiers:
hull[["edges"]]
## [,1] [,2]
## [1,] 2 3
## [2,] 2 4
## [3,] 2 6
## [4,] 3 5
## [5,] 3 7
## [6,] 4 5
## [7,] 4 8
## [8,] 5 9
## [9,] 6 7
## [10,] 6 8
## [11,] 7 9
## [12,] 8 9The ridges are given as a list:
hull[["ridges"]][[1]]
## $id
## [1] 1
##
## $ridgeOf
## [1] 1 4
##
## $vertices
## [1] 2 4The vertices field provides the vertices identifiers of
the ridge. A ridge is between two facets; the identifiers of these
facets are given in the field ridgeOf.
Facets are given as a list:
hull[["facets"]][[1]]
## $vertices
## [1] 8 4 6 2
##
## $edges
## [,1] [,2]
## [1,] 2 4
## [2,] 2 6
## [3,] 4 8
## [4,] 6 8
##
## $ridges
## [1] 1 2 3 4
##
## $neighbors
## [1] 2 3 4 5
##
## $volume
## [1] 1
##
## $center
## [1] 0.5 0.5 0.0
##
## $normal
## [1] 0 0 -1
##
## $offset
## [1] 0
##
## $family
## [1] NA
##
## $orientation
## [1] 1There is no id field for the facets: the integer
i is the identifier of the i-th facet of the
list.
The orientation field has two possible values,
1 or -1, it indicates the orientation of the
facet. See the plotting example below.
Here, the family field is NA for every
facet:
sapply(hull[["facets"]], `[[`, "family")
## [1] NA NA NA NA NA NAThis field has a possibly non-missing value only when one requires the triangulation of the convex hull:
thull <- cxhull(points, triangulate = TRUE)
sapply(thull[["facets"]], `[[`, "family")
## [1] 0 0 2 2 4 4 6 6 8 8 10 10The hull is triangulated into 12 triangles: each face of the cube is triangulated into two triangles. Therefore one gets six different families, each one consisting of two triangles: two triangles belong to the same family mean that they are parts of the same facet of the non-triangulated hull.
Observe the vertices of the first face of the cube:
hull[["facets"]][[1]][["vertices"]]
## [1] 8 4 6 2They are given as 8-4-6-2. They are not ordered, in the
sense that 4-6 and 2-8 are not edges of this
face:
( face_edges <- hull[["facets"]][[1]][["edges"]] )
## [,1] [,2]
## [1,] 2 4
## [2,] 2 6
## [3,] 4 8
## [4,] 6 8One can order the vertices as follows:
polygonize <- function(edges){
nedges <- nrow(edges)
vs <- edges[1, ]
v <- vs[2]
edges <- edges[-1, ]
for(. in 1:(nedges-2)){
j <- which(apply(edges, 1, function(e) v %in% e))
v <- edges[j, ][which(edges[j, ] != v)]
vs <- c(vs, v)
edges <- edges[-j, ]
}
vs
}
polygonize(face_edges)
## [1] 2 4 8 6Instead of using this function, use the hullMesh
function. It returns the vertices of the convex hull and its faces with
ordered indices.
cxhullEdges
functionThe cxhull function returns a lot of information about
the convex hull. If you only want to find the edges of the convex hull,
use the cxhullEdges function instead, for a speed gain and
less memory consumption. For example, the cxhull function
fails on my laptop for the E8
root polytope, while the cxhullEdges function works
(but it takes a while).
The package provides the function plotConvexHull3d to
plot a triangulated 3-dimensional hull with
rgl. Let’s take an icosidodecahedron as example:
library(cxhull)
library(rgl)
# icosidodecahedron
phi <- (1+sqrt(5))/2
vs1 <- rbind(
c(0, 0, 2*phi),
c(0, 2*phi, 0),
c(2*phi, 0, 0)
)
vs1 <- rbind(vs1, -vs1)
vs2 <- rbind(
c( 1, phi, phi^2),
c( 1, phi, -phi^2),
c( 1, -phi, phi^2),
c(-1, phi, phi^2),
c( 1, -phi, -phi^2),
c(-1, phi, -phi^2),
c(-1, -phi, phi^2),
c(-1, -phi, -phi^2)
)
vs2 <- rbind(vs2, vs2[, c(2, 3, 1)], vs2[, c(3, 1, 2)])
points <- rbind(vs1, vs2)
# computes the triangulated convex hull:
hull <- cxhull(points, triangulate = TRUE)# plot:
open3d(windowRect = c(50, 50, 562, 562))
view3d(10, 80, zoom = 0.7)
plotConvexHull3d(
hull, facesColor = "orangered", edgesColor = "yellow",
tubesRadius = 0.06, spheresRadius = 0.08
)
The plotConvexHull3d function calls the
TrianglesXYZ function, which takes care of the orientation
of the facets. Indeed, with the code below, we see the whole convex hull
while we hide the back side of the triangles:
triangles <- TrianglesXYZ(hull)
open3d(windowRect = c(50, 50, 562, 562))
view3d(10, 80, zoom = 0.7)
triangles3d(triangles, color = "green", back = "culled")
The orientation field of a facet indicates its
orientation (1 or -1).
There are three possiblities for the facesColor argument
of the plotConvexHull3d function. We have already seen the
first one: a single color. The second possibiity is to assign a color to
each triangle of the hull. There are 56 triangles:
length(hull[["facets"]])
## [1] 56So we specify 56 colors:
library(randomcoloR)
colors <- distinctColorPalette(56)
open3d(windowRect = c(50, 50, 562, 562))
view3d(10, 80, zoom = 0.7)
plotConvexHull3d(
hull, facesColor = colors, edgesColor = "yellow",
tubesRadius = 0.06, spheresRadius = 0.08
)
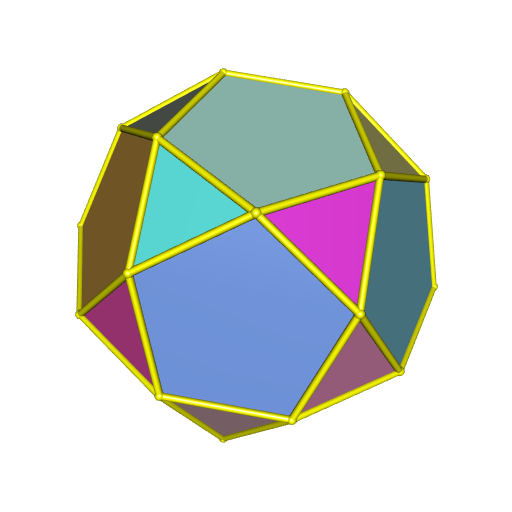
The third possibility is to assign a color to each face of the convex hull. There are 32 faces:
summary <- hullSummary(hull)
attr(summary, "facets")
## [1] "20 triangular facets, 12 other facets"library(randomcoloR)
colors <- distinctColorPalette(32)
open3d(windowRect = c(50, 50, 562, 562))
view3d(10, 80, zoom = 0.7)
plotConvexHull3d(
hull, facesColor = colors, edgesColor = "yellow",
tubesRadius = 0.06, spheresRadius = 0.08
)
Finally, instead of using the facesColor argument, you
can use the palette argument, which allows to decorate the
faces with a color gradient.
open3d(windowRect = c(50, 50, 562, 562))
view3d(10, 80, zoom = 0.7)
plotConvexHull3d(
hull, palette = hcl.colors(256, "BuPu"), bias = 0.25,
edgesColor = "yellow", tubesRadius = 0.06, spheresRadius = 0.08
)
Now, to illustrate the cxhull package, we deal with a
four-dimensional polytope: the truncated tesseract.
It is a convex polytope whose vertices are given by all permutations of (±1, ±(√2+1), ±(√2+1), ±(√2+1)).
Let’s enter these 64 vertices in a matrix points:
sqr2p1 <- sqrt(2) + 1
points <- rbind(
c(-1, -sqr2p1, -sqr2p1, -sqr2p1),
c(-1, -sqr2p1, -sqr2p1, sqr2p1),
c(-1, -sqr2p1, sqr2p1, -sqr2p1),
c(-1, -sqr2p1, sqr2p1, sqr2p1),
c(-1, sqr2p1, -sqr2p1, -sqr2p1),
c(-1, sqr2p1, -sqr2p1, sqr2p1),
c(-1, sqr2p1, sqr2p1, -sqr2p1),
c(-1, sqr2p1, sqr2p1, sqr2p1),
c(1, -sqr2p1, -sqr2p1, -sqr2p1),
c(1, -sqr2p1, -sqr2p1, sqr2p1),
c(1, -sqr2p1, sqr2p1, -sqr2p1),
c(1, -sqr2p1, sqr2p1, sqr2p1),
c(1, sqr2p1, -sqr2p1, -sqr2p1),
c(1, sqr2p1, -sqr2p1, sqr2p1),
c(1, sqr2p1, sqr2p1, -sqr2p1),
c(1, sqr2p1, sqr2p1, sqr2p1),
c(-sqr2p1, -1, -sqr2p1, -sqr2p1),
c(-sqr2p1, -1, -sqr2p1, sqr2p1),
c(-sqr2p1, -1, sqr2p1, -sqr2p1),
c(-sqr2p1, -1, sqr2p1, sqr2p1),
c(-sqr2p1, 1, -sqr2p1, -sqr2p1),
c(-sqr2p1, 1, -sqr2p1, sqr2p1),
c(-sqr2p1, 1, sqr2p1, -sqr2p1),
c(-sqr2p1, 1, sqr2p1, sqr2p1),
c(sqr2p1, -1, -sqr2p1, -sqr2p1),
c(sqr2p1, -1, -sqr2p1, sqr2p1),
c(sqr2p1, -1, sqr2p1, -sqr2p1),
c(sqr2p1, -1, sqr2p1, sqr2p1),
c(sqr2p1, 1, -sqr2p1, -sqr2p1),
c(sqr2p1, 1, -sqr2p1, sqr2p1),
c(sqr2p1, 1, sqr2p1, -sqr2p1),
c(sqr2p1, 1, sqr2p1, sqr2p1),
c(-sqr2p1, -sqr2p1, -1, -sqr2p1),
c(-sqr2p1, -sqr2p1, -1, sqr2p1),
c(-sqr2p1, -sqr2p1, 1, -sqr2p1),
c(-sqr2p1, -sqr2p1, 1, sqr2p1),
c(-sqr2p1, sqr2p1, -1, -sqr2p1),
c(-sqr2p1, sqr2p1, -1, sqr2p1),
c(-sqr2p1, sqr2p1, 1, -sqr2p1),
c(-sqr2p1, sqr2p1, 1, sqr2p1),
c(sqr2p1, -sqr2p1, -1, -sqr2p1),
c(sqr2p1, -sqr2p1, -1, sqr2p1),
c(sqr2p1, -sqr2p1, 1, -sqr2p1),
c(sqr2p1, -sqr2p1, 1, sqr2p1),
c(sqr2p1, sqr2p1, -1, -sqr2p1),
c(sqr2p1, sqr2p1, -1, sqr2p1),
c(sqr2p1, sqr2p1, 1, -sqr2p1),
c(sqr2p1, sqr2p1, 1, sqr2p1),
c(-sqr2p1, -sqr2p1, -sqr2p1, -1),
c(-sqr2p1, -sqr2p1, -sqr2p1, 1),
c(-sqr2p1, -sqr2p1, sqr2p1, -1),
c(-sqr2p1, -sqr2p1, sqr2p1, 1),
c(-sqr2p1, sqr2p1, -sqr2p1, -1),
c(-sqr2p1, sqr2p1, -sqr2p1, 1),
c(-sqr2p1, sqr2p1, sqr2p1, -1),
c(-sqr2p1, sqr2p1, sqr2p1, 1),
c(sqr2p1, -sqr2p1, -sqr2p1, -1),
c(sqr2p1, -sqr2p1, -sqr2p1, 1),
c(sqr2p1, -sqr2p1, sqr2p1, -1),
c(sqr2p1, -sqr2p1, sqr2p1, 1),
c(sqr2p1, sqr2p1, -sqr2p1, -1),
c(sqr2p1, sqr2p1, -sqr2p1, 1),
c(sqr2p1, sqr2p1, sqr2p1, -1),
c(sqr2p1, sqr2p1, sqr2p1, 1)
)As said before, the truncated tesseract is convex, therefore its
convex hull is itself. Let’s run the cxhull function on its
vertices:
library(cxhull)
hull <- cxhull(points)
str(hull, max = 1)
## List of 5
## $ vertices:List of 64
## $ edges : int [1:128, 1:2] 1 1 1 1 2 2 2 2 3 3 ...
## $ ridges :List of 88
## $ facets :List of 24
## $ volume : num 541We can observe that cxhull has not changed the order of
the points:
all(names(hull[["vertices"]]) == 1:64)
## [1] TRUELet’s look at the cells of the truncated tesseract:
table(sapply(hull[["facets"]], function(cell) length(cell[["ridges"]])))
##
## 4 14
## 16 8We see that 16 cells are made of 4 ridges; these cells are tetrahedra. We will draw them later, after projecting the truncated tesseract in the 3D-space.
For now, let’s draw the projected vertices and the edges.
The vertices in the 4D-space lie on the centered sphere with radius √(1+3(√2+1)2).
Therefore, a stereographic projection is appropriate to project the truncated tesseract in the 3D-space.
sproj <- function(p, r){
c(p[1], p[2], p[3])/(r - p[4])
}
ppoints <- t(apply(points, 1,
function(point) sproj(point, sqrt(1+3*sqr2p1^2))))Now we are ready to draw the projected vertices and the edges.
edges <- hull[["edges"]]
library(rgl)
open3d(windowRect = c(100, 100, 600, 600))
view3d(45, 45)
spheres3d(ppoints, radius = 0.07, color = "orange")
for(i in 1:nrow(edges)){
shade3d(cylinder3d(rbind(ppoints[edges[i, 1], ], ppoints[edges[i, 2], ]),
radius = 0.05, sides = 30), col = "gold")
}Pretty nice.
Now let’s show the 16 tetrahedra. Their faces correspond to triangular ridges. So we get the 64 triangles as follows:
ridgeSizes <-
sapply(hull[["ridges"]], function(ridge) length(ridge[["vertices"]]))
triangles <- t(sapply(hull[["ridges"]][which(ridgeSizes == 3)],
function(ridge) ridge[["vertices"]]))
head(triangles)
## [,1] [,2] [,3]
## [1,] 1 17 33
## [2,] 1 17 49
## [3,] 1 33 49
## [4,] 17 33 49
## [5,] 12 44 60
## [6,] 12 28 44We finally add the triangles:
for(i in 1:nrow(triangles)){
triangles3d(rbind(
ppoints[triangles[i, 1], ],
ppoints[triangles[i, 2], ],
ppoints[triangles[i, 3], ]),
color = "red", alpha = 0.4)
}We could also use different colors for the tetrahedra:
open3d(windowRect = c(100, 100, 600, 600))
view3d(45, 45)
spheres3d(ppoints, radius= 0.07, color = "orange")
for(i in 1:nrow(edges)){
shade3d(cylinder3d(rbind(ppoints[edges[i, 1], ], ppoints[edges[i, 2], ]),
radius = 0.05, sides = 30), col = "gold")
}
cellSizes <- sapply(hull[["facets"]], function(cell) length(cell[["ridges"]]))
tetrahedra <- hull[["facets"]][which(cellSizes == 4)]
colors <- rainbow(16)
for(i in seq_along(tetrahedra)){
triangles <- tetrahedra[[i]][["ridges"]]
for(j in 1:4){
triangle <- hull[["ridges"]][[triangles[j]]][["vertices"]]
triangles3d(rbind(
ppoints[triangle[1], ],
ppoints[triangle[2], ],
ppoints[triangle[3], ]),
color = colors[i], alpha = 0.4)
}
}These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.