The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
diffeqr is a package for solving differential equations in R. It utilizes DifferentialEquations.jl for its core routines to give high performance solving of ordinary differential equations (ODEs), stochastic differential equations (SDEs), delay differential equations (DDEs), and differential-algebraic equations (DAEs) directly in R.
If you have any questions, or just want to chat about solvers/using the package, please feel free to chat in the Zulip channel. For bug reports, feature requests, etc., please submit an issue.
diffeqr is registered into CRAN. Thus to add the package, use:
To install the master branch of the package (for developers), use:
Note that the first invocation of diffeqr::diffeq_setup() will install both Julia and the required packages if they are missing. If you wish to have it use an existing Julia binary, make sure that julia is found in the path. For more information see the julia_setup() function from JuliaCall.
As a demonstration, check out the following notebooks:
diffeqr provides a direct wrapper over DifferentialEquations.jl. The namespace is setup so that the standard syntax of Julia translates directly over to the R environment. There are two things to keep in mind:
de$! are replaced with _bang, for example solve! becomes solve_bang.Let’s solve the linear ODE u'=1.01u. First setup the package:
Define the derivative function f(u,p,t).
Then we give it an initial condition and a time span to solve over:
With those pieces we define the ODEProblem and solve the ODE:
This gives back a solution object for which sol$t are the time points and sol$u are the values. We can treat the solution as a continuous object in time via
and a high order interpolation will compute the value at t=0.2. We can check the solution by plotting it:
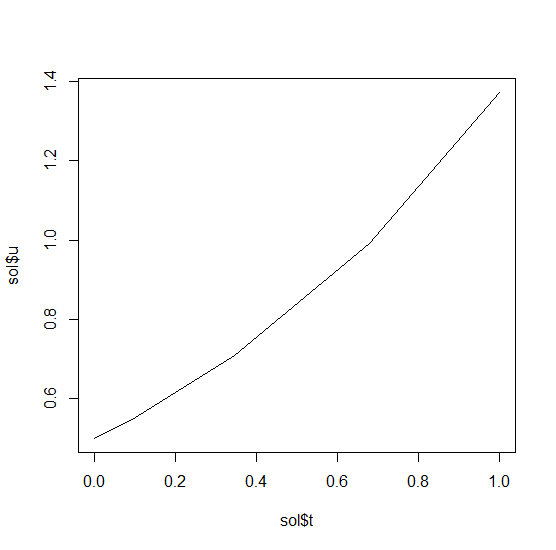
Now let’s solve the Lorenz equations. In this case, our initial condition is a vector and our derivative functions takes in the vector to return a vector (note: arbitrary dimensional arrays are allowed). We would define this as:
f <- function(u,p,t) {
du1 = p[1]*(u[2]-u[1])
du2 = u[1]*(p[2]-u[3]) - u[2]
du3 = u[1]*u[2] - p[3]*u[3]
return(c(du1,du2,du3))
}Here we utilized the parameter array p. Thus we use diffeqr::ode.solve like before, but also pass in parameters this time:
u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(f, u0, tspan, p)
sol <- de$solve(prob)The returned solution is like before except now sol$u is an array of arrays, where sol$u[i] is the full system at time sol$t[i]. It can be convenient to turn this into an R matrix through sapply:
This has each row as a time series. t(mat) makes each column a time series. It is sometimes convenient to turn the output into a data.frame which is done via:
Now we can use matplot to plot the timeseries together:
Now we can use the Plotly package to draw a phase plot:
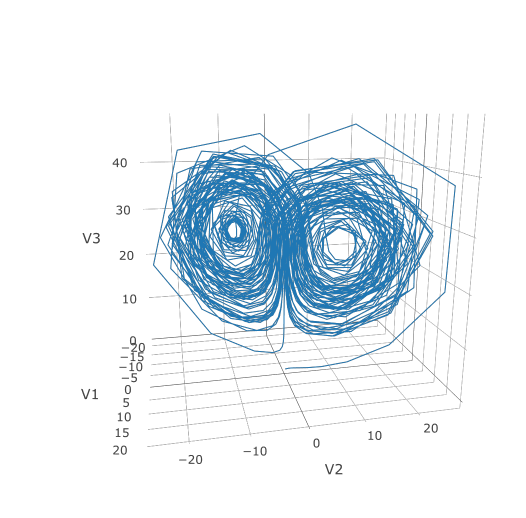
Plotly is much prettier!
If we want to have a more accurate solution, we can send abstol and reltol. Defaults are 1e-6 and 1e-3 respectively. Generally you can think of the digits of accuracy as related to 1 plus the exponent of the relative tolerance, so the default is two digits of accuracy. Absolute tolernace is the accuracy near 0.
In addition, we may want to choose to save at more time points. We do this by giving an array of values to save at as saveat. Together, this looks like:
abstol <- 1e-8
reltol <- 1e-8
saveat <- 0:10000/100
sol <- de$solve(prob,abstol=abstol,reltol=reltol,saveat=saveat)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')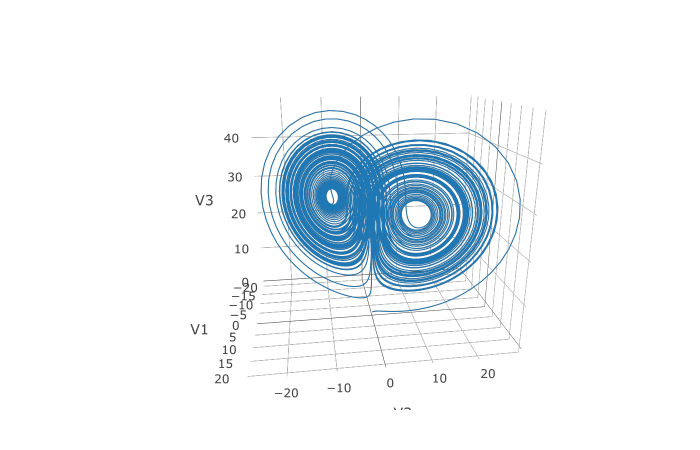
We can also choose to use a different algorithm. The choice is done using a string that matches the Julia syntax. See the ODE tutorial for details. The list of choices for ODEs can be found at the ODE Solvers page. For example, let’s use a 9th order method due to Verner:
Note that each algorithm choice will cause a JIT compilation.
One way to enhance the performance of your code is to define the function in Julia so that way it is JIT compiled. diffeqr is built using the JuliaCall package, and so you can utilize the Julia JIT compiler. We expose this automatically over ODE functions via jitoptimize_ode, like in the following example:
f <- function(u,p,t) {
du1 = p[1]*(u[2]-u[1])
du2 = u[1]*(p[2]-u[3]) - u[2]
du3 = u[1]*u[2] - p[3]*u[3]
return(c(du1,du2,du3))
}
u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(f, u0, tspan, p)
fastprob <- diffeqr::jitoptimize_ode(de,prob)
sol <- de$solve(fastprob,de$Tsit5())Note that the first evaluation of the function will have an ~2 second lag since the compiler will run, and all subsequent runs will be orders of magnitude faster than the pure R function. This means it’s great for expensive functions (ex. large PDEs) or functions called repeatedly, like during optimization of parameters.
We can also use the JuliaCall functions to directly define the function in Julia to eliminate the R interpreter overhead and get full JIT compilation:
julf <- JuliaCall::julia_eval("
function julf(du,u,p,t)
du[1] = 10.0*(u[2]-u[1])
du[2] = u[1]*(28.0-u[3]) - u[2]
du[3] = u[1]*u[2] - (8/3)*u[3]
end")
JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("p", p)
JuliaCall::julia_assign("tspan", tspan)
prob3 = JuliaCall::julia_eval("ODEProblem(julf, u0, tspan, p)")
sol = de$solve(prob3,de$Tsit5())To demonstrate the performance advantage, let’s time them all:
> system.time({ for (i in 1:100){ de$solve(prob ,de$Tsit5()) }})
user system elapsed
6.69 0.06 6.78
> system.time({ for (i in 1:100){ de$solve(fastprob,de$Tsit5()) }})
user system elapsed
0.11 0.03 0.14
> system.time({ for (i in 1:100){ de$solve(prob3 ,de$Tsit5()) }})
user system elapsed
0.14 0.02 0.15This is about a 50x improvement!
Using Julia’s ModelingToolkit for tracing to JIT compile via Julia has a few known limitations:
cos and sin all fall into this category. Notably, matrix multiplication is not supported.Solving stochastic differential equations (SDEs) is the similar to ODEs. To solve an SDE, you use diffeqr::sde.solve and give two functions: f and g, where du = f(u,t)dt + g(u,t)dW_t
de <- diffeqr::diffeq_setup()
f <- function(u,p,t) {
return(1.01*u)
}
g <- function(u,p,t) {
return(0.87*u)
}
u0 <- 1/2
tspan <- c(0.0,1.0)
prob <- de$SDEProblem(f,g,u0,tspan)
sol <- de$solve(prob)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = sol$t, y = sol$u, type = 'scatter', mode = 'lines')
Let’s add diagonal multiplicative noise to the Lorenz attractor. diffeqr defaults to diagonal noise when a system of equations is given. This is a unique noise term per system variable. Thus we generalize our previous functions as follows:
f <- function(u,p,t) {
du1 = p[1]*(u[2]-u[1])
du2 = u[1]*(p[2]-u[3]) - u[2]
du3 = u[1]*u[2] - p[3]*u[3]
return(c(du1,du2,du3))
}
g <- function(u,p,t) {
return(c(0.3*u[1],0.3*u[2],0.3*u[3]))
}
u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,1.0)
p <- c(10.0,28.0,8/3)
prob <- de$SDEProblem(f,g,u0,tspan,p)
sol <- de$solve(prob,saveat=0.005)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')Using a JIT compiled function for the drift and diffusion functions can greatly enhance the speed here. With the speed increase we can comfortably solve over long time spans:
tspan <- c(0.0,100.0)
prob <- de$SDEProblem(f,g,u0,tspan,p)
fastprob <- diffeqr::jitoptimize_sde(de,prob)
sol <- de$solve(fastprob,saveat=0.005)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')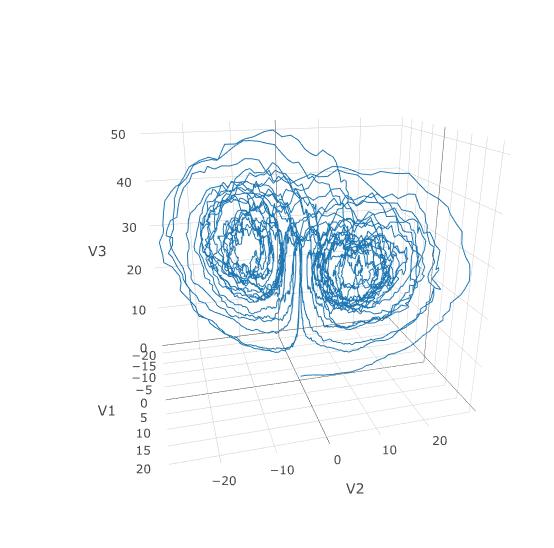
Let’s see how much faster the JIT-compiled version was:
> system.time({ for (i in 1:5){ de$solve(prob ) }})
user system elapsed
146.40 0.75 147.22
> system.time({ for (i in 1:5){ de$solve(fastprob) }})
user system elapsed
1.07 0.10 1.17Holy Monster’s Inc. that’s about 145x faster.
In many cases you may want to share noise terms across the system. This is known as non-diagonal noise. The DifferentialEquations.jl SDE Tutorial explains how the matrix form of the diffusion term corresponds to the summation style of multiple Wiener processes. Essentially, the row corresponds to which system the term is applied to, and the column is which noise term. So du[i,j] is the amount of noise due to the jth Wiener process that’s applied to u[i]. We solve the Lorenz system with correlated noise as follows:
f <- JuliaCall::julia_eval("
function f(du,u,p,t)
du[1] = 10.0*(u[2]-u[1])
du[2] = u[1]*(28.0-u[3]) - u[2]
du[3] = u[1]*u[2] - (8/3)*u[3]
end")
g <- JuliaCall::julia_eval("
function g(du,u,p,t)
du[1,1] = 0.3u[1]
du[2,1] = 0.6u[1]
du[3,1] = 0.2u[1]
du[1,2] = 1.2u[2]
du[2,2] = 0.2u[2]
du[3,2] = 0.3u[2]
end")
u0 <- c(1.0,0.0,0.0)
tspan <- c(0.0,100.0)
noise_rate_prototype <- matrix(c(0.0,0.0,0.0,0.0,0.0,0.0), nrow = 3, ncol = 2)
JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("tspan", tspan)
JuliaCall::julia_assign("noise_rate_prototype", noise_rate_prototype)
prob <- JuliaCall::julia_eval("SDEProblem(f, g, u0, tspan, p, noise_rate_prototype=noise_rate_prototype)")
sol <- de$solve(prob)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = ~V1, y = ~V2, z = ~V3, type = 'scatter3d', mode = 'lines')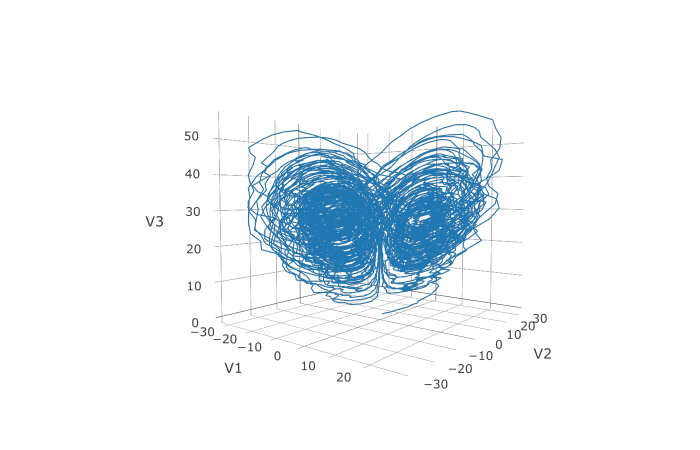
Here you can see that the warping effect of the noise correlations is quite visible! Note that we applied JIT compilation since it’s quite necessary for any difficult stochastic example.
A differential-algebraic equation is defined by an implicit function f(du,u,p,t)=0. All of the controls are the same as the other examples, except here you define a function which returns the residuals for each part of the equation to define the DAE. The initial value u0 and the initial derivative du0 are required, though they do not necessarily have to satisfy f (known as inconsistent initial conditions). The methods will automatically find consistent initial conditions. In order for this to occur, differential_vars must be set. This vector states which of the variables are differential (have a derivative term), with false meaning that the variable is purely algebraic.
This example shows how to solve the Robertson equation:
f <- function (du,u,p,t) {
resid1 = - 0.04*u[1] + 1e4*u[2]*u[3] - du[1]
resid2 = + 0.04*u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
resid3 = u[1] + u[2] + u[3] - 1.0
c(resid1,resid2,resid3)
}
u0 <- c(1.0, 0, 0)
du0 <- c(-0.04, 0.04, 0.0)
tspan <- c(0.0,100000.0)
differential_vars <- c(TRUE,TRUE,FALSE)
prob <- de$DAEProblem(f,du0,u0,tspan,differential_vars=differential_vars)
sol <- de$solve(prob)
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |>
plotly::add_trace(y = ~V2) |>
plotly::add_trace(y = ~V3)Additionally, an in-place JIT compiled form for f can be used to enhance the speed:
f = JuliaCall::julia_eval("function f(out,du,u,p,t)
out[1] = - 0.04u[1] + 1e4*u[2]*u[3] - du[1]
out[2] = + 0.04u[1] - 3e7*u[2]^2 - 1e4*u[2]*u[3] - du[2]
out[3] = u[1] + u[2] + u[3] - 1.0
end")
u0 <- c(1.0, 0, 0)
du0 <- c(-0.04, 0.04, 0.0)
tspan <- c(0.0,100000.0)
differential_vars <- c(TRUE,TRUE,FALSE)
JuliaCall::julia_assign("du0", du0)
JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("p", p)
JuliaCall::julia_assign("tspan", tspan)
JuliaCall::julia_assign("differential_vars", differential_vars)
prob = JuliaCall::julia_eval("DAEProblem(f, du0, u0, tspan, p, differential_vars=differential_vars)")
sol = de$solve(prob)
A delay differential equation is an ODE which allows the use of previous values. In this case, the function needs to be a JIT compiled Julia function. It looks just like the ODE, except in this case there is a function h(p,t) which allows you to interpolate and grab previous values.
We must provide a history function h(p,t) that gives values for u before t0. Here we assume that the solution was constant before the initial time point. Additionally, we pass constant_lags = c(20.0) to tell the solver that only constant-time lags were used and what the lag length was. This helps improve the solver accuracy by accurately stepping at the points of discontinuity. Together this is:
f <- JuliaCall::julia_eval("function f(du, u, h, p, t)
du[1] = 1.1/(1 + sqrt(10)*(h(p, t-20)[1])^(5/4)) - 10*u[1]/(1 + 40*u[2])
du[2] = 100*u[1]/(1 + 40*u[2]) - 2.43*u[2]
end")
h <- JuliaCall::julia_eval("function h(p, t)
[1.05767027/3, 1.030713491/3]
end")
u0 <- c(1.05767027/3, 1.030713491/3)
tspan <- c(0.0, 100.0)
constant_lags <- c(20.0)
JuliaCall::julia_assign("u0", u0)
JuliaCall::julia_assign("tspan", tspan)
JuliaCall::julia_assign("constant_lags", tspan)
prob <- JuliaCall::julia_eval("DDEProblem(f, u0, h, tspan, constant_lags = constant_lags)")
sol <- de$solve(prob,de$MethodOfSteps(de$Tsit5()))
udf <- as.data.frame(t(sapply(sol$u,identity)))
plotly::plot_ly(udf, x = sol$t, y = ~V1, type = 'scatter', mode = 'lines') |> plotly::add_trace(y = ~V2)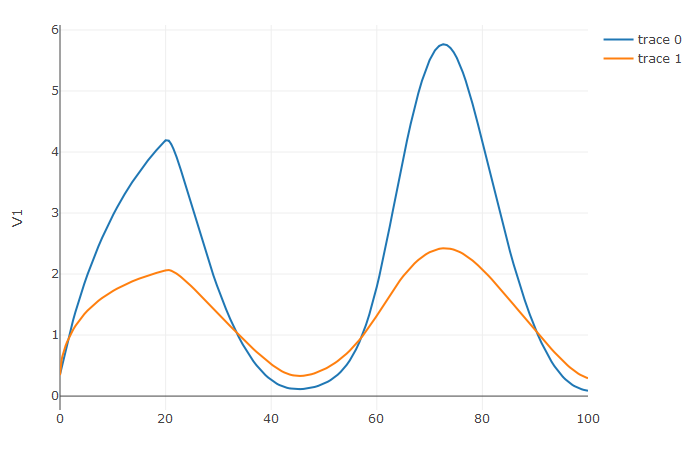
Notice that the solver accurately is able to simulate the kink (discontinuity) at t=20 due to the discontinuity of the derivative at the initial time point! This is why declaring discontinuities can enhance the solver accuracy.
In many cases one is interested in solving the same ODE many times over many different initial conditions and parameters. In diffeqr parlance this is called an ensemble solve. diffeqr inherits the parallelism tools of the SciML ecosystem that are used for things like automated equation discovery and acceleration. Here we will demonstrate using these parallel tools to accelerate the solving of an ensemble.
First, let’s define the JIT-accelerated Lorenz equation like before:
de <- diffeqr::diffeq_setup()
lorenz <- function (u,p,t){
du1 = p[1]*(u[2]-u[1])
du2 = u[1]*(p[2]-u[3]) - u[2]
du3 = u[1]*u[2] - p[3]*u[3]
c(du1,du2,du3)
}
u0 <- c(1.0,1.0,1.0)
tspan <- c(0.0,100.0)
p <- c(10.0,28.0,8/3)
prob <- de$ODEProblem(lorenz,u0,tspan,p)
fastprob <- diffeqr::jitoptimize_ode(de,prob)Now we use the EnsembleProblem as defined on the ensemble parallelism page of the documentation: Let’s build an ensemble by utilizing uniform random numbers to randomize the initial conditions and parameters:
prob_func <- function (prob,i,rep){
de$remake(prob,u0=runif(3)*u0,p=runif(3)*p)
}
ensembleprob = de$EnsembleProblem(fastprob, prob_func = prob_func, safetycopy=FALSE)Now we solve the ensemble in serial:
To add GPUs to the mix, we need to bring in DiffEqGPU. The diffeqr::diffeqgpu_setup() helper function will install CUDA for you and bring all of the bindings into the returned object:
diffeqr::diffeqgpu_setup can take awhile to run the first time as it installs the drivers!Now we simply use EnsembleGPUKernel(degpu$CUDABackend()) with a GPU-specialized ODE solver GPUTsit5() to solve 10,000 ODEs on the GPU in parallel:
For the full list of choices for specialized GPU solvers, see the DiffEqGPU.jl documentation.
Note that EnsembleGPUArray can be used as well, like:
though we highly recommend the EnsembleGPUKernel methods for more speed. Given the way the JIT compilation performed will also ensure that the faster kernel generation methods work, EnsembleGPUKernel is almost certainly the better choice in most applications.
To see how much of an effect the parallelism has, let’s test this against R’s deSolve package. This is exactly the same problem as the documentation example for deSolve, so let’s copy that verbatim and then add a function to do the ensemble generation:
library(deSolve)
Lorenz <- function(t, state, parameters) {
with(as.list(c(state, parameters)), {
dX <- a * X + Y * Z
dY <- b * (Y - Z)
dZ <- -X * Y + c * Y - Z
list(c(dX, dY, dZ))
})
}
parameters <- c(a = -8/3, b = -10, c = 28)
state <- c(X = 1, Y = 1, Z = 1)
times <- seq(0, 100, by = 0.01)
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
lorenz_solve <- function (i){
state <- c(X = runif(1), Y = runif(1), Z = runif(1))
parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
}Using lapply to generate the ensemble we get:
> system.time({ lapply(1:1000,lorenz_solve) })
user system elapsed
225.81 0.46 226.63Now let’s see how the JIT-accelerated serial Julia version stacks up against that:
> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=1000,saveat=0.01) })
user system elapsed
2.75 0.30 3.08Julia is already about 73x faster than the pure R solvers here! Now let’s add GPU-acceleration to the mix:
> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=1000,saveat=0.01) })
user system elapsed
0.11 0.00 0.12Already 26x times faster! But the GPU acceleration is made for massively parallel problems, so let’s up the trajectories a bit. We will not use more trajectories from R because that would take too much computing power, so let’s see what happens to the Julia serial and GPU at 10,000 trajectories:
> system.time({ de$solve(ensembleprob,de$Tsit5(),de$EnsembleSerial(),trajectories=10000,saveat=0.01) })
user system elapsed
35.02 4.19 39.25> system.time({ de$solve(ensembleprob,degpu$GPUTsit5(),degpu$EnsembleGPUKernel(degpu$CUDABackend()),trajectories=10000,saveat=0.01) })
user system elapsed
1.22 0.23 1.50 To compare this to the pure Julia code:
using OrdinaryDiffEq, DiffEqGPU, CUDA, StaticArrays
function lorenz(u, p, t)
σ = p[1]
ρ = p[2]
β = p[3]
du1 = σ * (u[2] - u[1])
du2 = u[1] * (ρ - u[3]) - u[2]
du3 = u[1] * u[2] - β * u[3]
return SVector{3}(du1, du2, du3)
end
u0 = SA[1.0f0; 0.0f0; 0.0f0]
tspan = (0.0f0, 10.0f0)
p = SA[10.0f0, 28.0f0, 8 / 3.0f0]
prob = ODEProblem{false}(lorenz, u0, tspan, p)
prob_func = (prob, i, repeat) -> remake(prob, p = (@SVector rand(Float32, 3)) .* p)
monteprob = EnsembleProblem(prob, prob_func = prob_func, safetycopy = false)
@time sol = solve(monteprob, GPUTsit5(), EnsembleGPUKernel(CUDA.CUDABackend()),
trajectories = 10_000,
saveat = 1.0f0);
# 0.015064 seconds (257.68 k allocations: 13.132 MiB)which is about two orders of magnitude faster for computing 10,000 trajectories, note that the major factors are that we cannot define 32-bit floating point values from R and the prob_func for generating the initial conditions and parameters is a major bottleneck since this function is written in R.
To see how this scales in Julia, let’s take it to insane heights. First, let’s reduce the amount we’re saving:
@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=10_000,saveat=1.0f0)
0.015040 seconds (257.64 k allocations: 13.130 MiB)This highlights that controlling memory pressure is key with GPU usage: you will get much better performance when requiring less saved points on the GPU.
@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=100_000,saveat=1.0f0)
# 0.150901 seconds (2.60 M allocations: 131.576 MiB)compared to serial:
@time sol = solve(monteprob,Tsit5(),EnsembleSerial(),trajectories=100_000,saveat=1.0f0)
# 22.136743 seconds (16.40 M allocations: 1.628 GiB, 42.98% gc time)And now we start to see that scaling power! Let’s solve 1 million trajectories:
@time sol = solve(monteprob,GPUTsit5(),EnsembleGPUKernel(CUDA.CUDABackend()),trajectories=1_000_000,saveat=1.0f0)
# 1.031295 seconds (3.40 M allocations: 241.075 MiB)For reference, let’s look at deSolve with the change to only save that much:
times <- seq(0, 100, by = 1.0)
lorenz_solve <- function (i){
state <- c(X = runif(1), Y = runif(1), Z = runif(1))
parameters <- c(a = -8/3 * runif(1), b = -10 * runif(1), c = 28 * runif(1))
out <- ode(y = state, times = times, func = Lorenz, parms = parameters)
}
system.time({ lapply(1:1000,lorenz_solve) }) user system elapsed
49.69 3.36 53.42 The GPU version is solving 1000x as many trajectories, 50x as fast! So conclusion, if you need the most speed, you may want to move to the Julia version to get the most out of your GPU due to Float32’s, and when using GPUs make sure it’s a problem with a relatively average or low memory pressure, and these methods will give orders of magnitude acceleration compared to what you might be used to.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.