The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
The ebrahim.gof package implements the Ebrahim-Farrington goodness-of-fit test for logistic regression models. This test is particularly effective for binary data and sparse datasets, providing an improved alternative to the traditional Hosmer-Lemeshow test.
Copy and paste this in R or R-studio.
# Install devtools if you haven't already
if (!requireNamespace("devtools", quietly = TRUE)) {
install.packages("devtools")
}
# Install ebrahim.gof from GitHub
devtools::install_github("ebrahimkhaled/ebrahim.gof")Another way to install the R-Libarary, but its not availabe yet.
# Will be available after CRAN submission
install.packages("ebrahim.gof")library(ebrahim.gof)
# Example with binary data
set.seed(123)
n <- 500
x <- rnorm(n)
linpred <- 0.5 + 1.2 * x
prob <- 1 / (1 + exp(-linpred))
y <- rbinom(n, 1, prob)
# Fit logistic regression
model <- glm(y ~ x, family = binomial())
predicted_probs <- fitted(model)
# Perform Ebrahim-Farrington test
result <- ef.gof(y, predicted_probs, G = 10)
print(result)ef.gof()The main function that performs the goodness-of-fit test:
ef.gof(y, predicted_probs , G = 10, model = NULL, m = NULL)Parameters: - y: Binary response vector
(0/1) or success counts for grouped data - predicted_probs:
Vector of predicted probabilities from logistic model - G:
Number of groups for binary data (default: 10) - model:
Optional glm object (required for original Farrington only, not for
Ebrahim-Farrington test) - m: Optional vector of trial
counts (for grouped data) (required for original Farrington only, not
for Ebrahim-Farrington test)
Returns: A data frame with test name, test statistic, and p-value.
library(ebrahim.gof)
# Simulate binary data
set.seed(42)
n <- 1000
x1 <- rnorm(n)
x2 <- rnorm(n)
linpred <- -0.5 + 0.8 * x1 + 0.6 * x2
prob <- plogis(linpred)
y <- rbinom(n, 1, prob)
# Fit logistic regression
model <- glm(y ~ x1 + x2, family = binomial())
predicted_probs <- fitted(model)
# Test goodness of fit
result <- ef.gof(y, predicted_probs, G = 10)
print(result)
#> Test Test_Statistic p_value
#> 1 Ebrahim-Farrington -0.8944 0.8143# Test with different numbers of groups
results <- data.frame(
Groups = c(4, 10, 20),
P_value = c(
ef.gof(y, predicted_probs, G = 4)$p_value,
ef.gof(y, predicted_probs, G = 10)$p_value,
ef.gof(y, predicted_probs, G = 20)$p_value
)
)
print(results)library(ResourceSelection)
# Ebrahim-Farrington test
ef_result <- ef.gof(y, predicted_probs, G = 10)
# Hosmer-Lemeshow test
hl_result <- hoslem.test(y, predicted_probs, g = 10)
# Compare results
comparison <- data.frame(
Test = c("Ebrahim-Farrington", "Hosmer-Lemeshow"),
P_value = c(ef_result$p_value, hl_result$p.value)
)
print(comparison)# Function to simulate misspecified model
simulate_power <- function(n, beta_quad = 0.1, n_sims = 100) {
rejections <- 0
for (i in 1:n_sims) {
x <- runif(n, -2, 2)
# True model has quadratic term
linpred_true <- 0 + x + beta_quad * x^2
prob_true <- plogis(linpred_true)
y <- rbinom(n, 1, prob_true)
# Fit misspecified linear model
model_mis <- glm(y ~ x, family = binomial())
pred_probs <- fitted(model_mis)
# Test goodness of fit
test_result <- ef.gof(y, pred_probs, G = 10)
if (test_result$p_value < 0.05) {
rejections <- rejections + 1
}
}
return(rejections / n_sims)
}
# Calculate power for different sample sizes
power_results <- data.frame(
n = c(100, 200, 500, 1000),
power = sapply(c(100, 200, 500, 1000), simulate_power)
)
print(power_results)The Ebrahim-Farrington test is based on Farrington’s (1996) theoretical framework but simplified for practical implementation with binary data. The test uses a modified Pearson chi-square statistic:
For binary data with automatic grouping, the test statistic is:
Z_EF = (T_EF - (G - 2)) / sqrt(2(G - 2))Where: - T_EF is the modified Pearson chi-square
statistic - G is the number of groups - The test statistic
follows a standard normal distribution under H₀

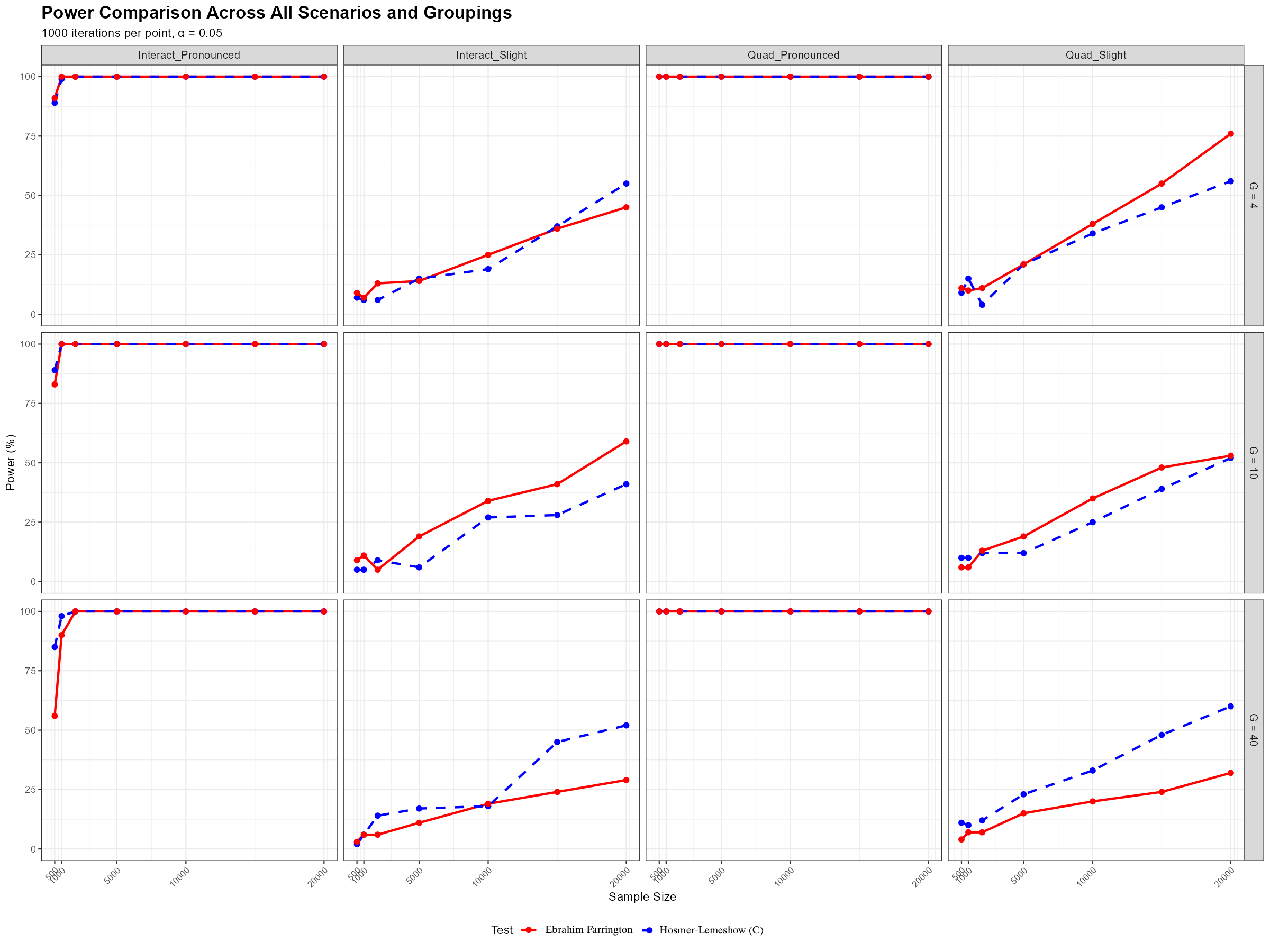
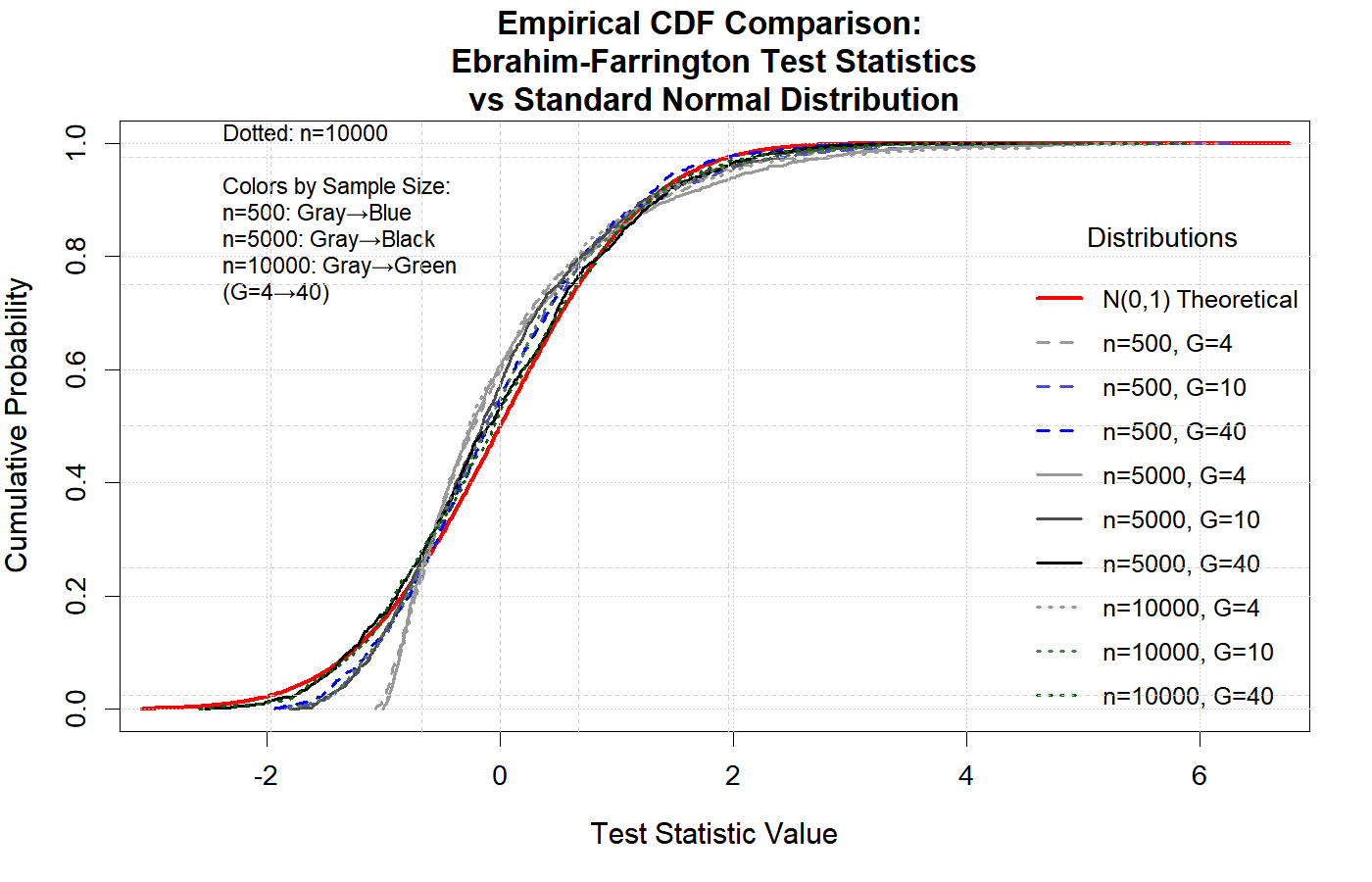
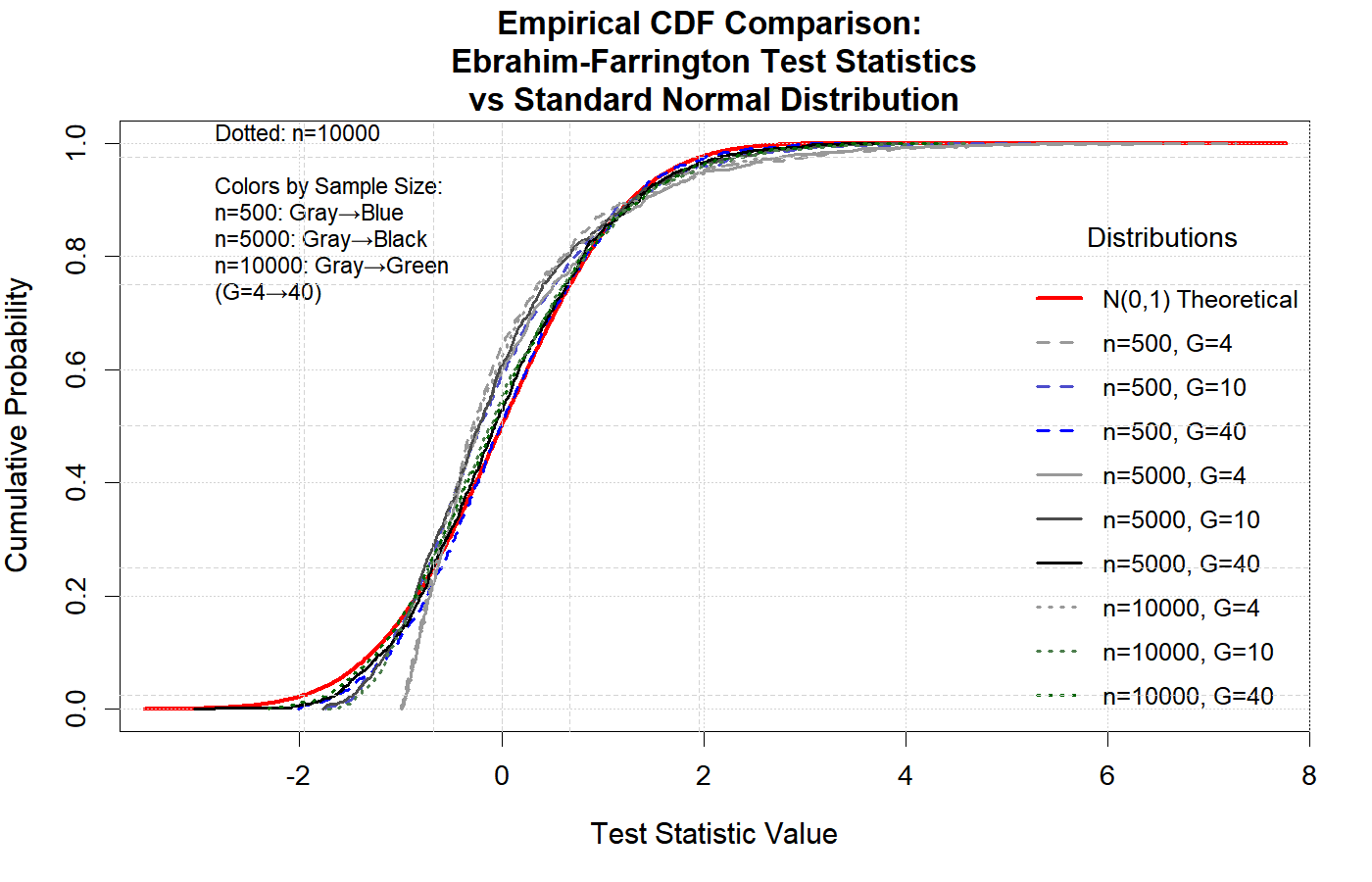
The following two figures illustrate that, under the null hypothesis, the Ebrahim-Farrington test statistic is asymptotically standard normal for both single-predictor and multiple-predictor logistic regression models. This property holds even in sparse data settings, confirming the theoretical foundation of the test and supporting its use for model assessment. (see (Ebrahim,2025))
These results demonstrate that the Ebrahim-Farrington test maintains the correct type I error rate and its statistic converges to the standard normal distribution as sample size increases, validating its asymptotic properties.
Farrington, C. P. (1996). On Assessing Goodness of Fit of Generalized Linear Models to Sparse Data. Journal of the Royal Statistical Society. Series B (Methodological), 58(2), 349-360.
Ebrahim, Khaled Ebrahim (2025). Goodness-of-Fits Tests and Calibration Machine Learning Algorithms for Logistic Regression Model with Sparse Data. Master’s Thesis, Alexandria University.
Hosmer, D. W., & Lemeshow, S. (2000). Applied Logistic Regression, Second Edition. New York: Wiley.
If you use this package in your research, please cite:
Ebrahim, K. E. (2025). ebrahim.gof: Ebrahim-Farrington Goodness-of-Fit Test
for Logistic Regression. R package version 1.0.0.
https://github.com/ebrahimkhaled/ebrahim.gofContributions are welcome! Please feel free to submit a Pull Request. For major changes, please open an issue first to discuss what you would like to change.
This project is licensed under the GPL-3 License
Ebrahim Khaled Ebrahim
Alexandria University
Email: ebrahimkhaled@alexu.edu.eg
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.