The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
The goal of ewp is to provide a modelling interface for
underdispersed count data based on the exponentially weighted Poisson
(EWP) distribution described by Ridout & Besbeas (2004), allowing
for nest-level covariates on the location parameter of the EWP. Currently only the
three-parameter version of the distribution (EWP_3) is implemented.
You can install the development version of ewp directly from github like so (requires a working C++ compiler toolchain):
remotes::install_github('pboesu/ewp')The package contains a reconstructed version of the linnet dataset from Ridout & Besbeas (2004), which consists of 5414 clutch size records and is augmented with two synthetic covariates, one that is random noise, and one that is correlated with clutch size. The parameter estimates for the intercept-only model presented in Ridout & Besbeas (2004) can be reproduced like so:
library(ewp)
fit_null <- ewp_reg(eggs ~ 1, data = linnet)# this may take a few seconds
#> start values are:
#> (Intercept) beta1 beta2
#> 1.546823 0.000000 0.000000
#> initial value 9530.456809
#> iter 4 value 5324.797069
#> iter 8 value 5299.393228
#> final value 5299.362098
#> converged
#>
#> Calculating Hessian. This may take a while.
summary(fit_null)
#> Deviance residuals:
#>
#> lambda coefficients (ewp3 with log link):
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.584650 0.003511 451.3 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> dispersion coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> beta1 1.46441 0.05588 26.21 <2e-16 ***
#> beta2 2.35681 0.05607 42.04 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Number of iterations in optimization: 11
#> Log-likelihood: -5299 on 3 DfNote that the linear predictor on uses a log-link.
A model with nest-level covariates can be fitted by specifying a more
complex model formula - as in the base R glm()
fit <- ewp_reg(eggs ~ cov1 + cov2, data = linnet)# this may take 5-10 seconds
#> start values are:
#> (Intercept) cov1 cov2 beta1 beta2
#> 1.204279467 -0.001259307 0.071872488 0.000000000 0.000000000
#> initial value 9434.616462
#> iter 4 value 5054.429651
#> iter 8 value 4596.004461
#> iter 12 value 4440.611768
#> iter 16 value 4423.783976
#> iter 20 value 4420.081202
#> iter 20 value 4420.081199
#> iter 20 value 4420.081199
#> final value 4420.081199
#> converged
#>
#> Calculating Hessian. This may take a while.
summary(fit)
#> Deviance residuals:
#>
#> lambda coefficients (ewp3 with log link):
#> Estimate Std. Error z value Pr(>|z|)
#> (Intercept) 1.3335734 0.0048514 274.883 <2e-16 ***
#> cov1 -0.0007823 0.0014025 -0.558 0.577
#> cov2 0.0532956 0.0009553 55.791 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> dispersion coefficients:
#> Estimate Std. Error z value Pr(>|z|)
#> beta1 1.89858 0.04404 43.11 <2e-16 ***
#> beta2 3.05108 0.08761 34.83 <2e-16 ***
#> ---
#> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#>
#> Number of iterations in optimization: 20
#> Log-likelihood: -4420 on 5 DfSimulation based residual diagnostics are indirectly available
through the package DHARMa, by using
the simulate.ewp method:
library(DHARMa)
#> Warning: package 'DHARMa' was built under R version 4.2.2
#> This is DHARMa 0.4.6. For overview type '?DHARMa'. For recent changes, type news(package = 'DHARMa')
#simulate from fitted model
sims <- simulate(fit, nsim = 20)
#create a DHARMa abject
DH <- createDHARMa(simulatedResponse = as.matrix(sims),#simulated responses
observedResponse = linnet$eggs,#original response
fittedPredictedResponse = fit$fitted.values,#fitted values from ewp model
integerResponse = T)#tell DHARMa this is a discrete probability distribution
#plot diagnostics
plot(DH)
#> DHARMa:testOutliers with type = binomial may have inflated Type I error rates for integer-valued distributions. To get a more exact result, it is recommended to re-run testOutliers with type = 'bootstrap'. See ?testOutliers for details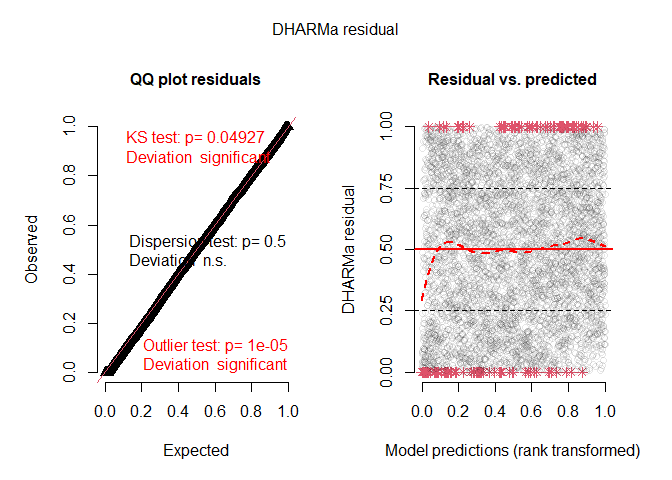
:warning: Note that the maximum likelihood optimisation procedure is still experimental :warning:
In particular:
- At the moment the likelihood evaluation is optimised for small
counts ( << 20) and uses a hard upper
limit of 30 for potential counts, this means the model is
currently only suitable for datasets with expected counts up to 20-25,
depending on the degree of underdispersion. A warning is issued if this
criterion in not met when using
ewp_reg(), but other
functions may fail silently. - Fitting is very slow (think minutes, not
seconds), especially when estimating the Hessian matrix for more than a
couple of parameters! - Estimates may not be stable for models with many
covariates and/or very large sample sizes (1000s). Centering and
scaling continuous covariates seems to help on that front.
:warning::warning::warning:
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.