The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

HMMs for Finance

The {fHMM} R package allows for the detection and characterization of financial market regimes in time series data by applying hidden Markov Models (HMMs). The vignettes outline the package functionality and the model formulation.

For a reference on the method, see:

Oelschläger, L., and Adam, T. 2021. “Detecting Bearish and Bullish Markets in Financial Time Series Using Hierarchical Hidden Markov Models.” Statistical Modelling. https://doi.org/10.1177/1471082X211034048

A user guide is provided by the accompanying software paper:

Oelschläger, L., Adam, T., and Michels, R. 2024. “fHMM: Hidden Markov Models for Financial Time Series in R”. Journal of Statistical Software. https://doi.org/10.18637/jss.v109.i09

Below, we illustrate an application to the German stock index DAX. We also show how to use the package to simulate HMM data, compute the model likelihood, and decode the hidden states using the Viterbi algorithm.

Installation

You can install the released package version from CRAN with:

install.packages("fHMM")

Contributing

We are open to contributions and would appreciate your input:

If you encounter any issues, please submit bug reports as issues.
If you have any ideas for new features, please submit them as feature requests.
If you would like to add extensions to the package, please fork the master branch and submit a merge request.

Example: Fitting an HMM to the DAX

We fit a 3-state HMM with state-dependent t-distributions to the DAX log-returns from 2000 to 2022. The states can be interpreted as proxies for bearish (green below) and bullish markets (red) and an “in-between” market state (yellow).

library("fHMM")

The package has a build-in function to download financial data from Yahoo Finance:

dax <- download_data(symbol = "^GDAXI")

We first need to define the model:

controls <- set_controls(
  states      = 3,
  sdds        = "t",
  file        = dax,
  date_column = "Date",
  data_column = "Close",
  logreturns  = TRUE,
  from        = "2000-01-01",
  to          = "2022-12-31"
)

The function prepare_data() then prepares the data for estimation:

data <- prepare_data(controls)

The summary() method gives an overview:

summary(data)
#> Summary of fHMM empirical data
#> * number of observations: 5882 
#> * data source: data.frame 
#> * date column: Date 
#> * log returns: TRUE

We fit the model and subsequently decode the hidden states and compute (pseudo-) residuals:

model <- fit_model(data)
model <- decode_states(model)
model <- compute_residuals(model)

The summary() method gives an overview of the model fit:

summary(model)
#> Summary of fHMM model
#> 
#>   simulated hierarchy       LL       AIC       BIC
#> 1     FALSE     FALSE 17650.02 -35270.05 -35169.85
#> 
#> State-dependent distributions:
#> t() 
#> 
#> Estimates:
#>                   lb   estimate        ub
#> Gamma_2.1  2.754e-03  5.024e-03 9.110e-03
#> Gamma_3.1  2.808e-16  2.781e-16 2.739e-16
#> Gamma_1.2  1.006e-02  1.839e-02 3.338e-02
#> Gamma_3.2  1.514e-02  2.446e-02 3.927e-02
#> Gamma_1.3  5.596e-17  5.549e-17 5.464e-17
#> Gamma_2.3  1.196e-02  1.898e-02 2.993e-02
#> mu_1      -3.862e-03 -1.793e-03 2.754e-04
#> mu_2      -7.994e-04 -2.649e-04 2.696e-04
#> mu_3       9.642e-04  1.272e-03 1.579e-03
#> sigma_1    2.354e-02  2.586e-02 2.840e-02
#> sigma_2    1.225e-02  1.300e-02 1.380e-02
#> sigma_3    5.390e-03  5.833e-03 6.312e-03
#> df_1       5.550e+00  1.084e+01 2.116e+01
#> df_2       6.785e+00  4.866e+01 3.489e+02
#> df_3       3.973e+00  5.248e+00 6.934e+00
#> 
#> States:
#> decoded
#>    1    2    3 
#>  704 2926 2252 
#> 
#> Residuals:
#>      Min.   1st Qu.    Median      Mean   3rd Qu.      Max. 
#> -3.517900 -0.664018  0.012170 -0.003262  0.673180  3.693568

Having estimated the model, we can visualize the state-dependent distributions and the decoded time series:

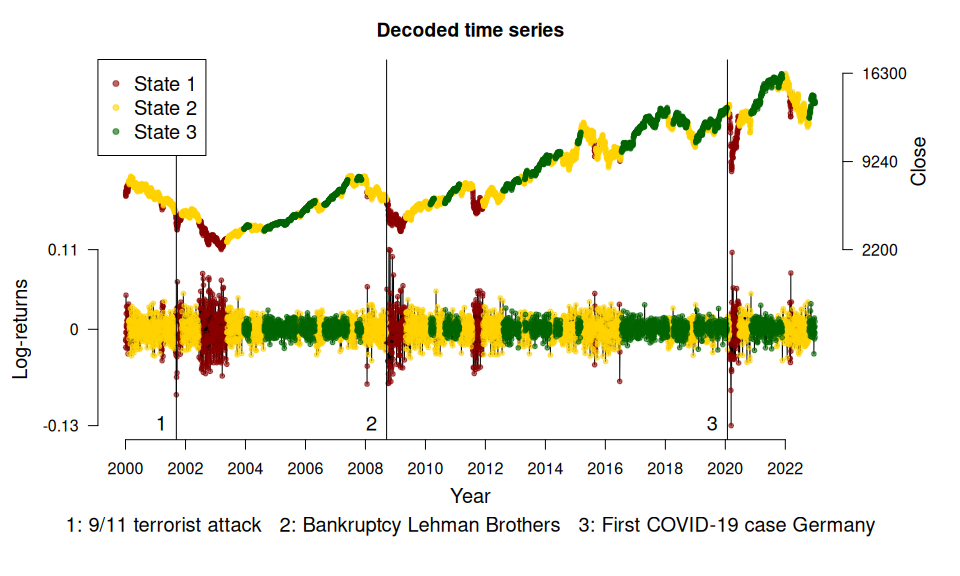
events <- fHMM_events(
  list(dates = c("2001-09-11", "2008-09-15", "2020-01-27"),
       labels = c("9/11 terrorist attack", "Bankruptcy Lehman Brothers", "First COVID-19 case Germany"))
)
plot(model, plot_type = c("sdds","ts"), events = events)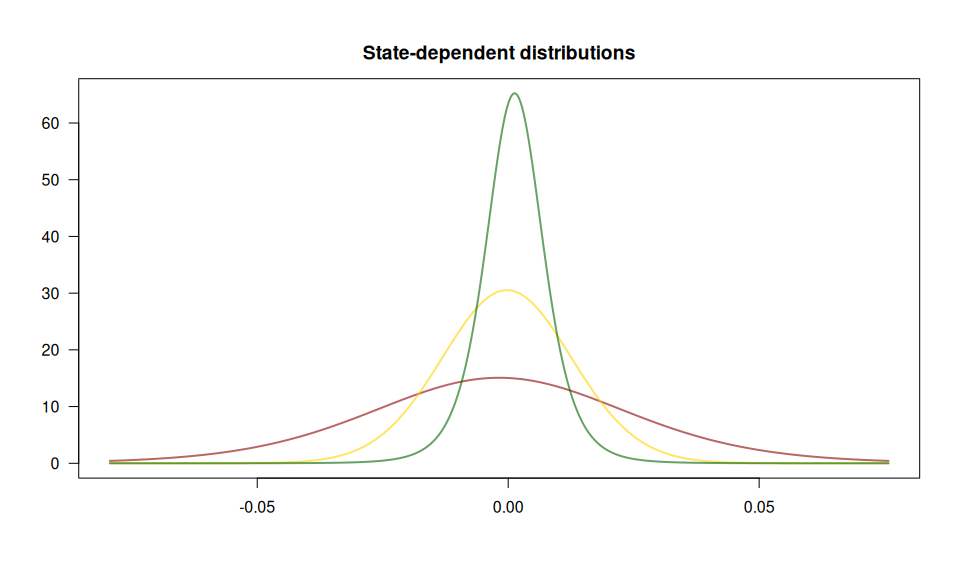

The (pseudo-) residuals help to evaluate the model fit:

plot(model, plot_type = "pr")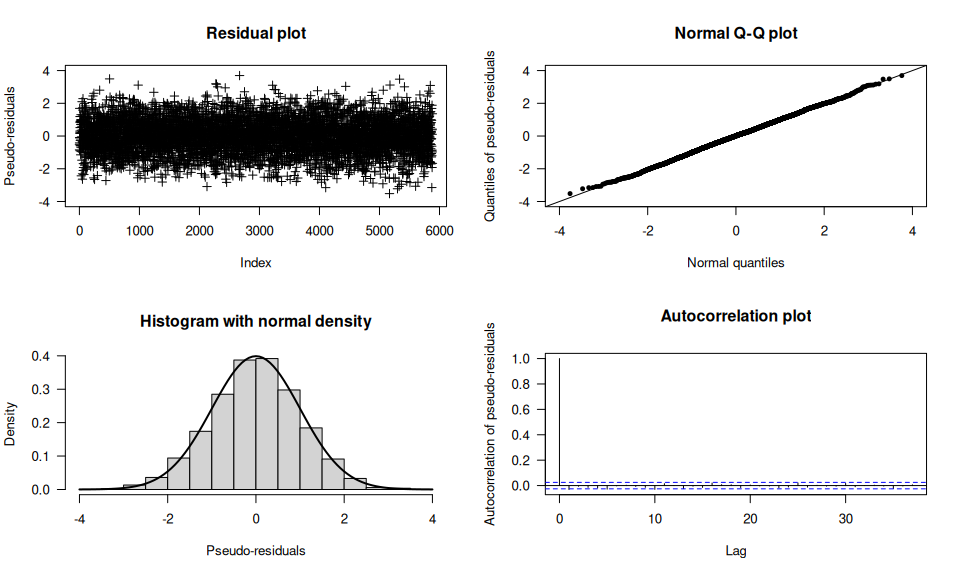

Simulating HMM data

The {fHMM} package supports data simulation from an HMM and access to the model likelihood function for model fitting and the Viterbi algorithm for state decoding.

As an example, we consider a 2-state HMM with state-dependent Gamma distributions and a time horizon of 1000 data points.

controls <- set_controls(
  states  = 2,
  sdds    = "gamma",
  horizon = 1000
)

Define the model parameters via the fHMM_parameters() function (unspecified parameters would be set at random).

par <- fHMM_parameters(
  controls = controls,
  Gamma    = matrix(c(0.95, 0.05, 0.05, 0.95), 2, 2), 
  mu       = c(1, 3), 
  sigma    = c(1, 3)
)

Simulate data points from this model via the simulate_hmm() function.

sim <- simulate_hmm(
  controls        = controls,
  true_parameters = par
)
plot(sim$data, col = sim$markov_chain, type = "b")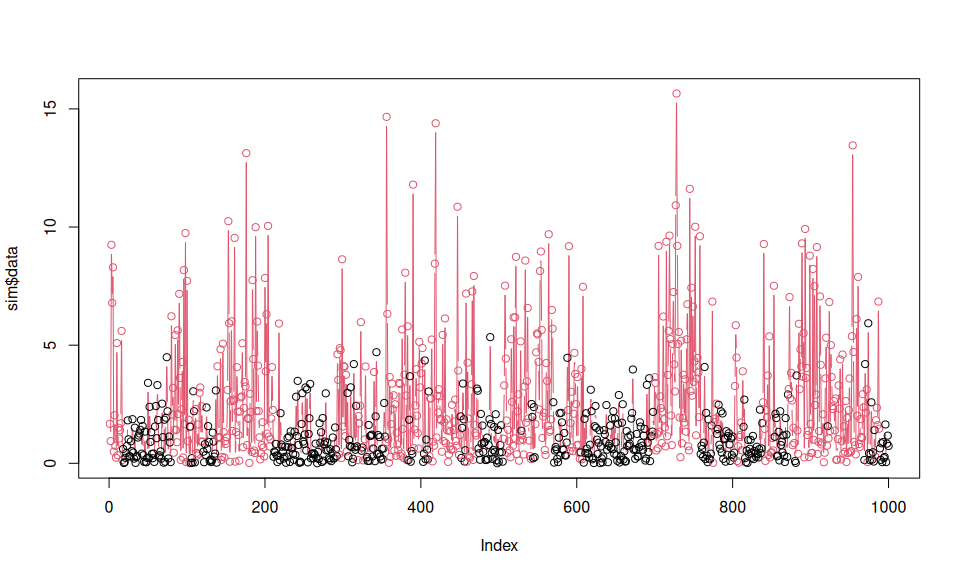

The log-likelihood function ll_hmm() is evaluated at the identified and unconstrained parameter values, they can be derived via the par2parUncon() function.

(parUncon <- par2parUncon(par, controls))
#> gammasUncon_21 gammasUncon_12      muUncon_1      muUncon_2   sigmaUncon_1 
#>      -2.944439      -2.944439       0.000000       1.098612       0.000000 
#>   sigmaUncon_2 
#>       1.098612 
#> attr(,"class")
#> [1] "parUncon" "numeric"

Note that this transformation takes care of the restrictions, that Gamma must be a transition probability matrix (which we can ensure via the logit link) and that mu and sigma must be positive (an assumption for the Gamma distribution, which we can ensure via the exponential link).

ll_hmm(parUncon, sim$data, controls)
#> [1] -1620.515

ll_hmm(parUncon, sim$data, controls, negative = TRUE)
#> [1] 1620.515

For maximum likelihood estimation of the model parameters, we can numerically optimize ll_hmm() over parUncon (or rather minimize the negative log-likelihood).

optimization <- nlm(
  f = ll_hmm, p = parUncon, observations = sim$data, controls = controls, negative = TRUE
)

(estimate <- optimization$estimate)
#> [1] -3.46338992 -3.44065582  0.05999848  1.06452907  0.11517811  1.07946252

To interpret the estimate, it needs to be back transformed to the constrained parameter space via the parUncon2par() function. The state-labeling is not identified.

class(estimate) <- "parUncon"
estimate <- parUncon2par(estimate, controls)

par$Gamma
#>         state_1 state_2
#> state_1    0.95    0.05
#> state_2    0.05    0.95

estimate$Gamma
#>            state_1    state_2
#> state_1 0.96895125 0.03104875
#> state_2 0.03037204 0.96962796


par$mu
#> muCon_1 muCon_2 
#>       1       3

estimate$mu
#>  muCon_1  muCon_2 
#> 1.061835 2.899473


par$sigma
#> sigmaCon_1 sigmaCon_2 
#>          1          3

estimate$sigma
#> sigmaCon_1 sigmaCon_2 
#>   1.122073   2.943097

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.