The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
While many awesome packages for network analysis exist for R, all with their own offerings and advantages, they also all have their own vocabulary, syntax, and expected formats for data inputs and analytic outputs. Many of these packages only work on some types of networks (usually one-mode, simple, directed or undirected networks) for some types of analysis; if you want to analyse a different type of network or try a different analysis, a different package is needed. And they can rely on a very different visual language (and sometimes plotting engine), which can mess up your pretty presentation or paper. This can make learning and using network analysis tools in R challenging.
By contrast, {manynet} offers many analytic
tools that work on many (if not most) types and kinds of
networks. It helps researchers make, modify, map, mark, measure, and
identify nodes’ motifs and memberships in networks. For further testing
and modelling capabilities, see {migraph} and
the other stocnet packages.
Networks can come from many sources and be found in many different
formats: some can be found in this or other packages, some can be
created or generated using functions in this package, and others can be
downloaded from the internet and imported from your file system.
{manynet} provides tools to make networks from all these
sources in any number of common formats.
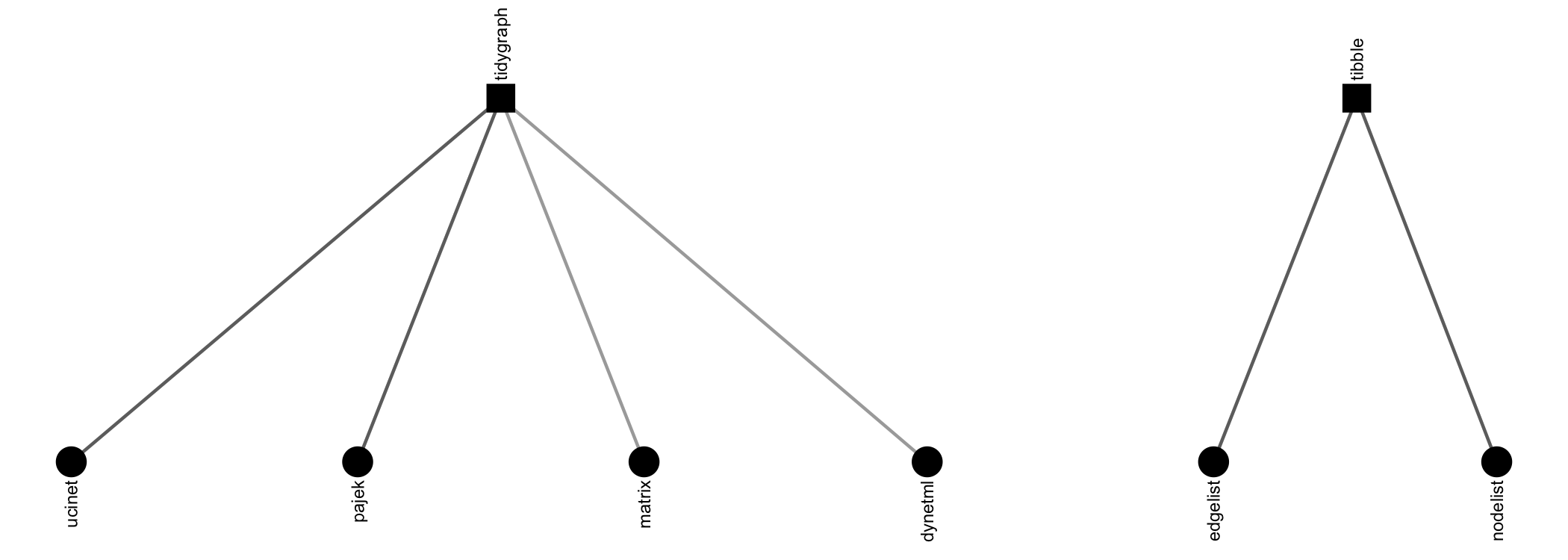
{manynet} offers a number of options for importing
network data found in other repositories. Besides importing and
exporting to Excel edgelists, nodelists, and (bi)adjacency matrices,
there are specific routines included for UCINET, Pajek, GraphML, and DynetML files,
e.g.:
If you cannot remember the file name/path, then just run
read_*() with the parentheses empty, and a file selection
popup will open so that you can browse through your file system to find
the file. Usually both read_*() and write_*()
are offered to make sure that {manynet} is compatible with
your larger project and analytic workflow.
read_cran(), read_dynetml(),
read_edgelist(), read_graphml(),
read_matrix(), read_nodelist(),
read_pajek(), read_ucinet()write_edgelist(), write_graphml(),
write_matrix(), write_nodelist(),
write_pajek(), write_ucinet()There may be no need to import network data though, if that network
data already exists in a package in R. To facilitate testing and to
contribute to an ecosystem of easily accessible network data,
particularly for pedagogical purposes, we include a number of classical
and instructional network datasets, all thoroughly documented and ready
for analysis. Here are just a few examples, all available in
{manynet}:
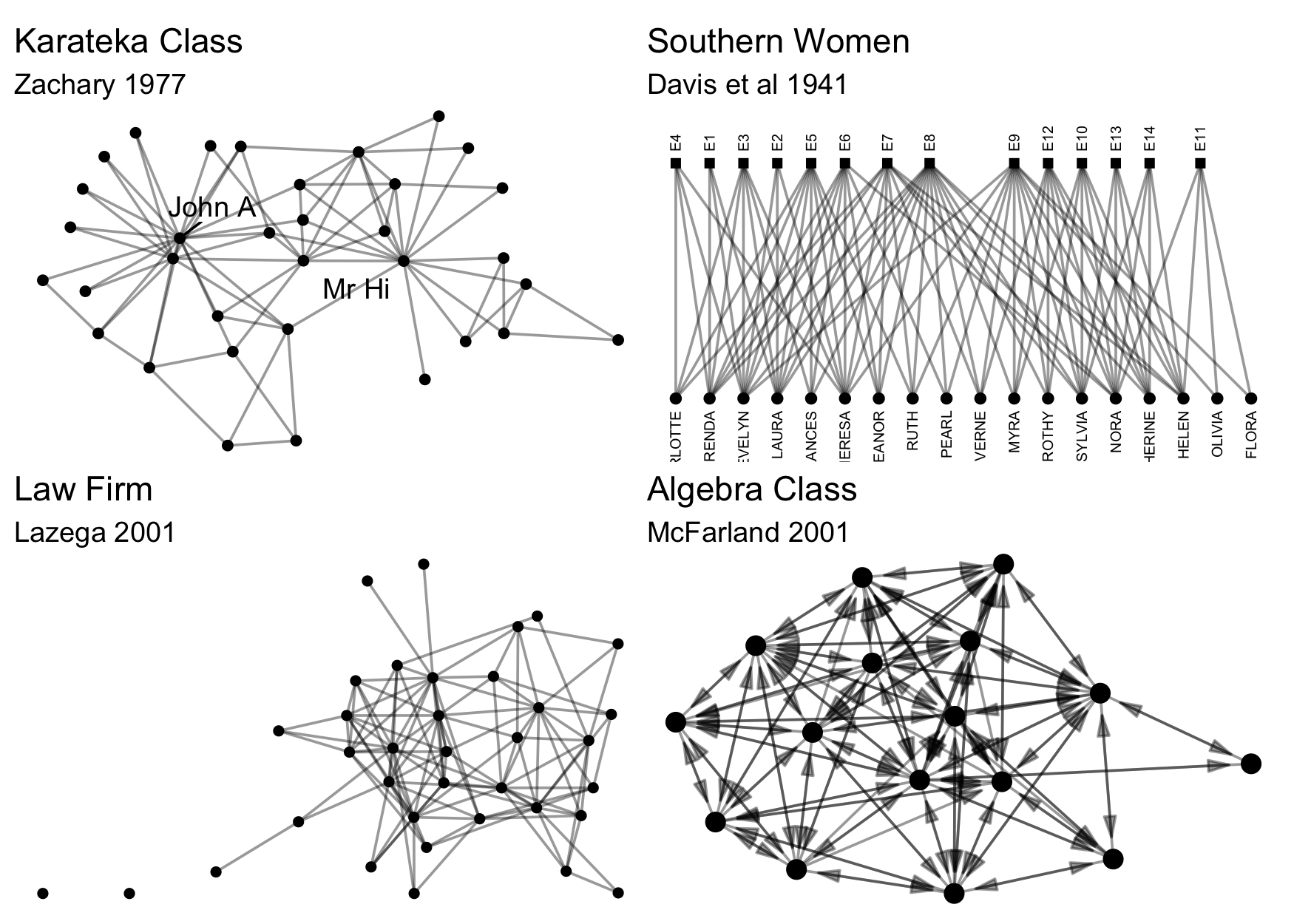
Here are some others: ison_adolescents,
ison_algebra, ison_brandes,
ison_friends, ison_greys,
ison_hightech, ison_karateka,
ison_koenigsberg, ison_laterals,
ison_lawfirm, ison_lotr,
ison_marvel_relationships, ison_marvel_teams,
ison_monks, ison_networkers,
ison_physicians, ison_potter,
ison_southern_women, ison_starwars,
ison_usstates
{manynet} includes functions for making networks
algorithmically. The create_* group of functions create
networks with a particular structure, and will always create the same
format from the same inputs, e.g.:
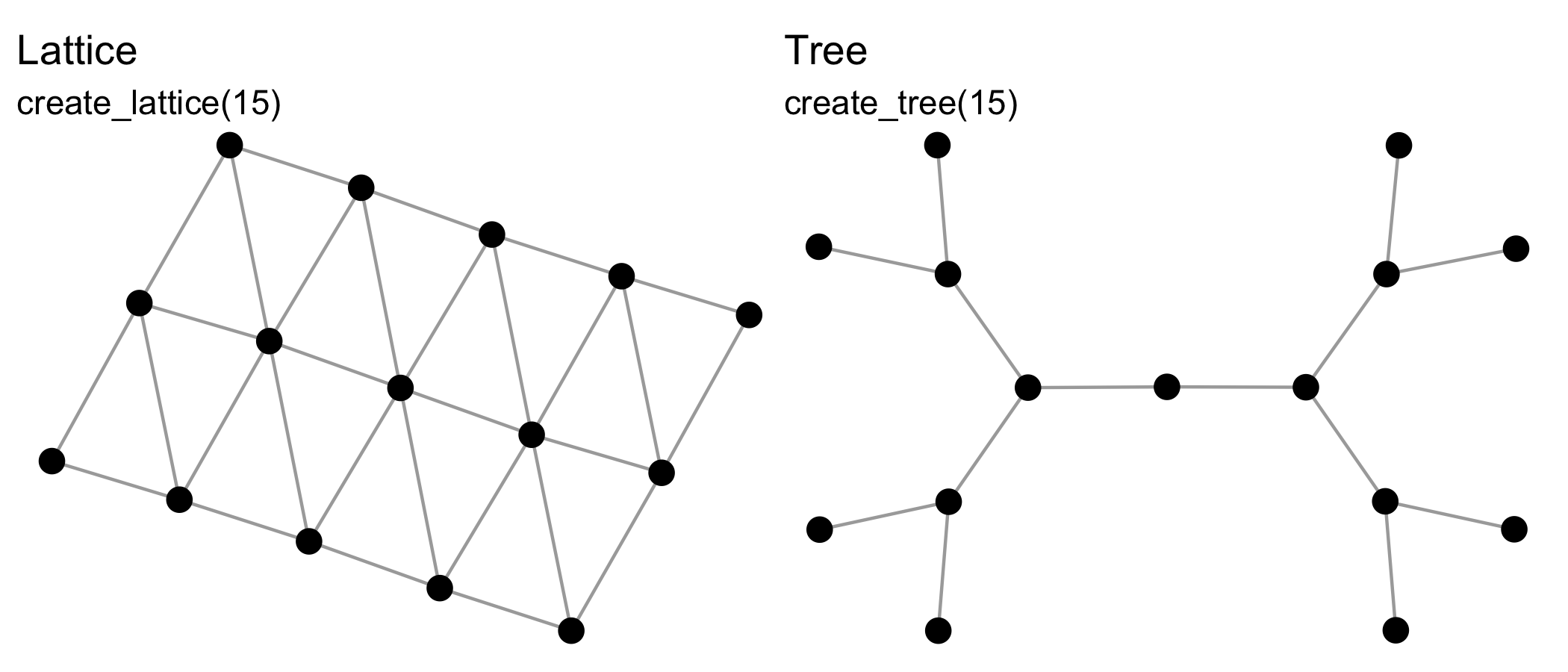
See also create_components(),
create_core(), create_degree(),
create_empty(), create_explicit(),
create_filled(), create_lattice(),
create_ring(), create_star(),
create_tree().
The generate_* group of functions generate networks from
generative mechanisms that may include some random aspect, and so will
return a different output each time they are run, e.g.:
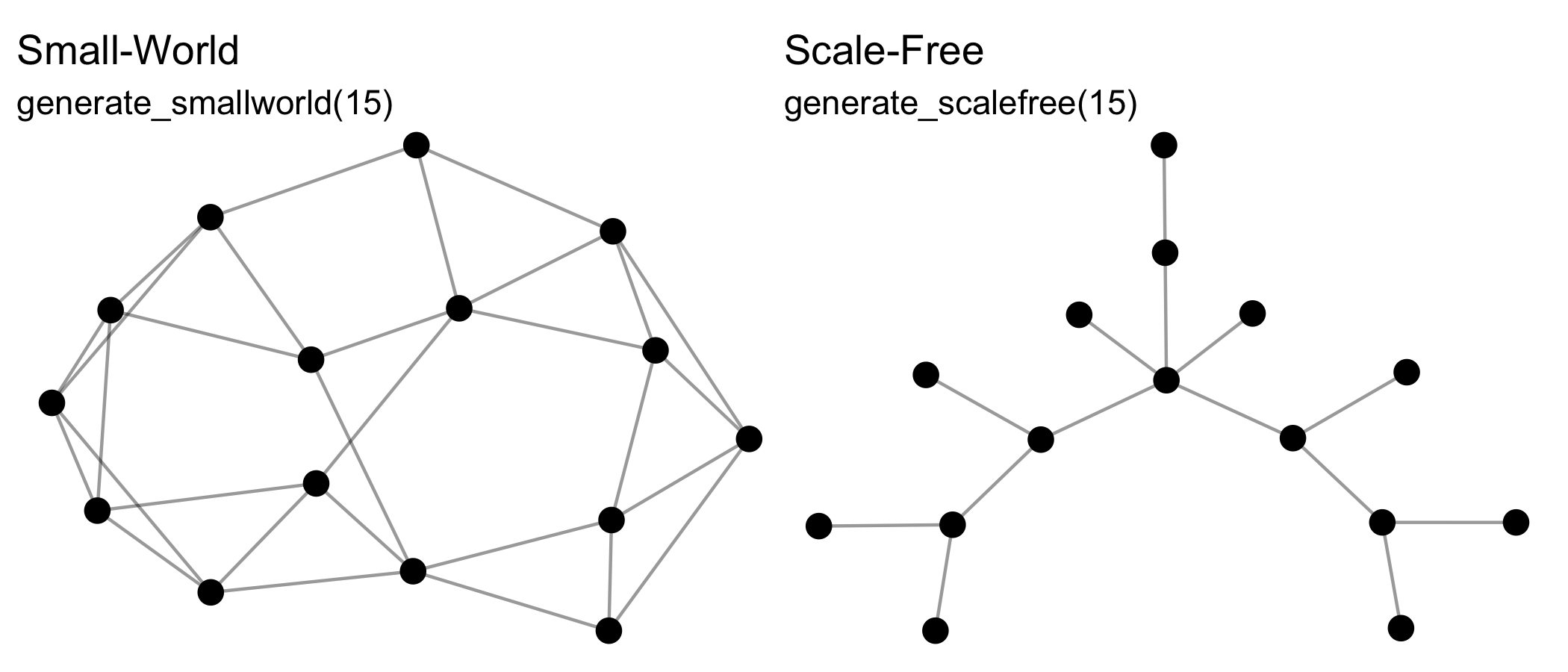
See also generate_citations(),
generate_configuration(), generate_fire(),
generate_islands(), generate_man(),
generate_permutation(), generate_random(),
generate_scalefree(), generate_smallworld(),
generate_utilities().
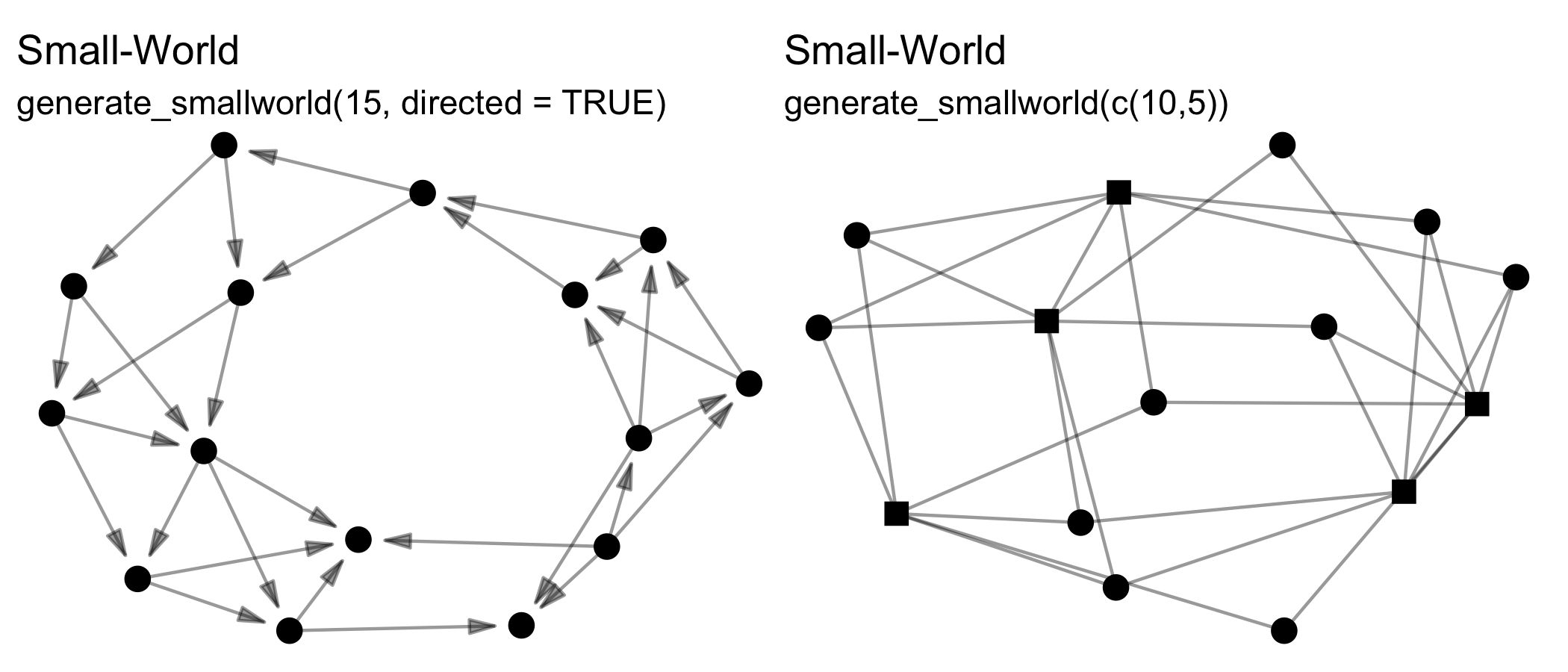
Note that all these functions can create directed or undirected,
one-mode or two-mode networks. Creating two-mode networks is as easy as
passing the first argument (n) a vector of two integers
instead of one. For example, while n = 15 will create a
one-mode network of 10 nodes, whereas n = c(10,5) will
create a two-mode network of 10 nodes in the first mode, and 5 nodes in
the second mode. Some of these functions wrap existing algorithms in
other packages, while others are unique offerings or add additional
formats, e.g. two-mode networks.
Lastly, {manynet} also includes functions for simulating
diffusion or learning processes over a given network:
play_diffusion(), play_diffusions(),
play_learning(), play_segregation()The diffusion models include not only SI and threshold models, but also SIS, SIR, SIRS, SEIR, and SEIRS.
Before or during analysis, you may need to modify the network you are
analysing in various ways. Different packages have different syntaxes
and vocabulary for such actions; {manynet}’s
to_*() functions can be used on any class object to
reformat, transform, or split networks into networks with other
properties.
Once you have imported network data, identified network data in this
or other packages in R, or invented your own, you may need to translate
this data into another class for analysis. {manynet}’s
as_*() functions can be used to coerce objects from one of
many common classes into any other. Below is a directed graph showing
the currently available options:
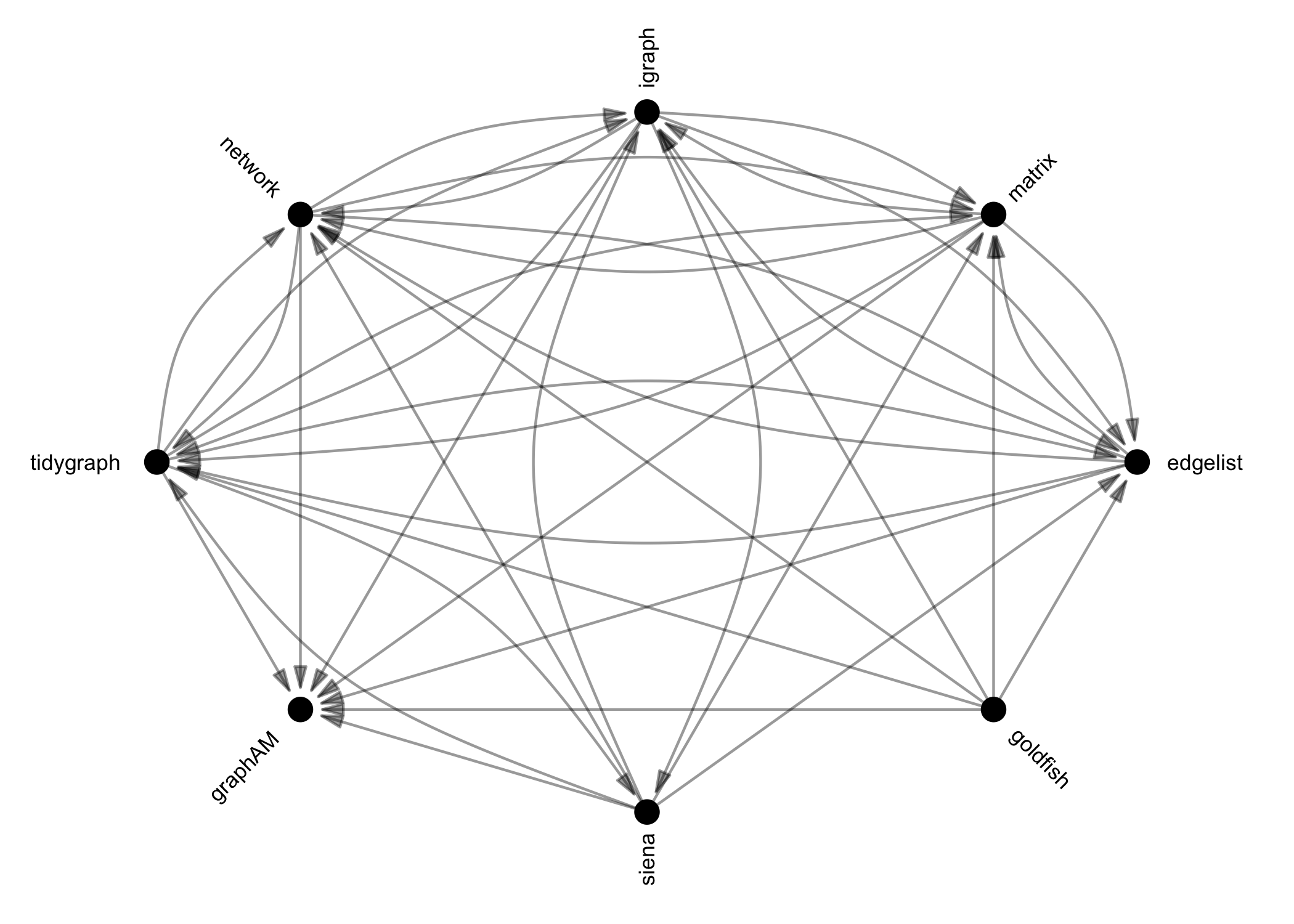
These functions are designed to be as intuitive and lossless as possible, outperforming many other class-coercion packages.
We use these functions internally in every {manynet} and
{migraph} function to (1) allow them to be run on any
compatible network format and (2) use the most efficient algorithm
available. This makes {manynet} and {migraph}
compatible with your existing workflow, whether you use base R matrices
or edgelists as data frames, {igraph}, {network}, or {tidygraph},
and extensible by developments in those other packages too.
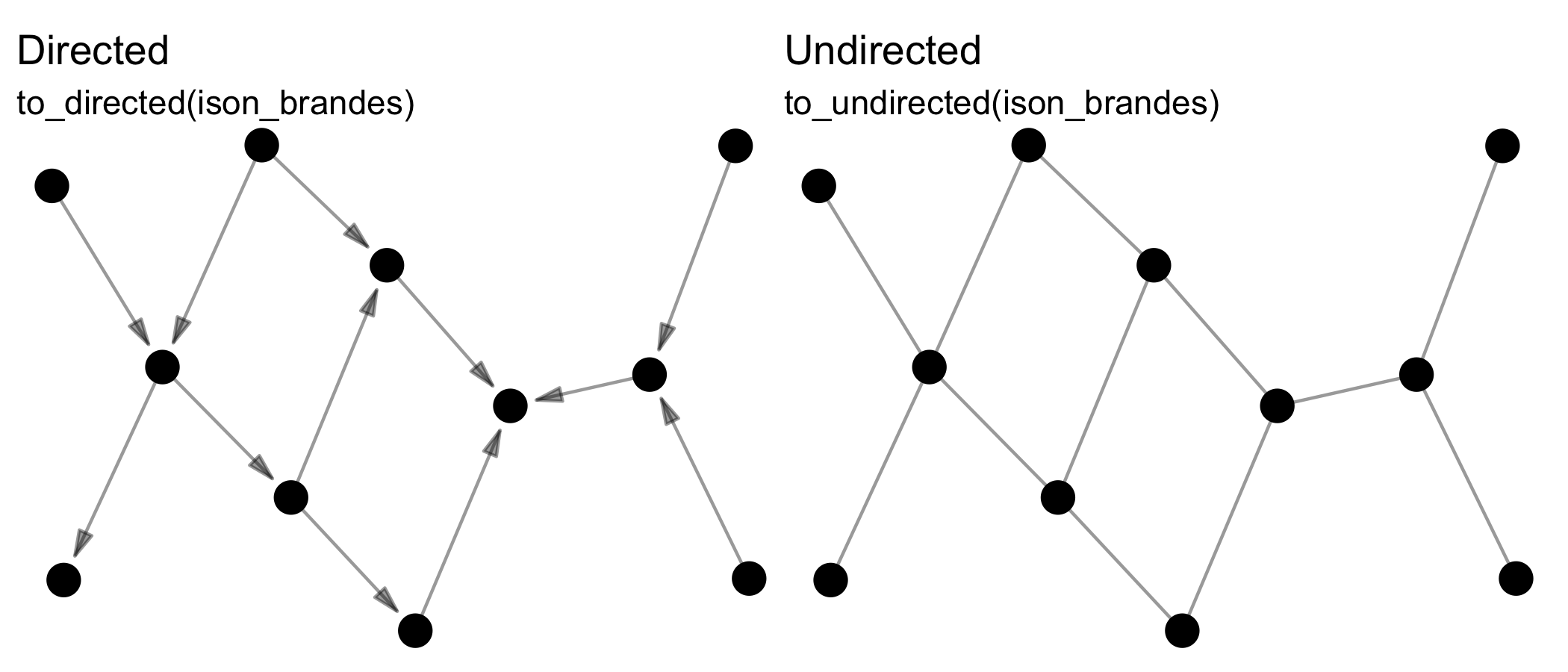
Reformatting means changing the format of the network, e.g. from
directed to undirected via to_undirected().
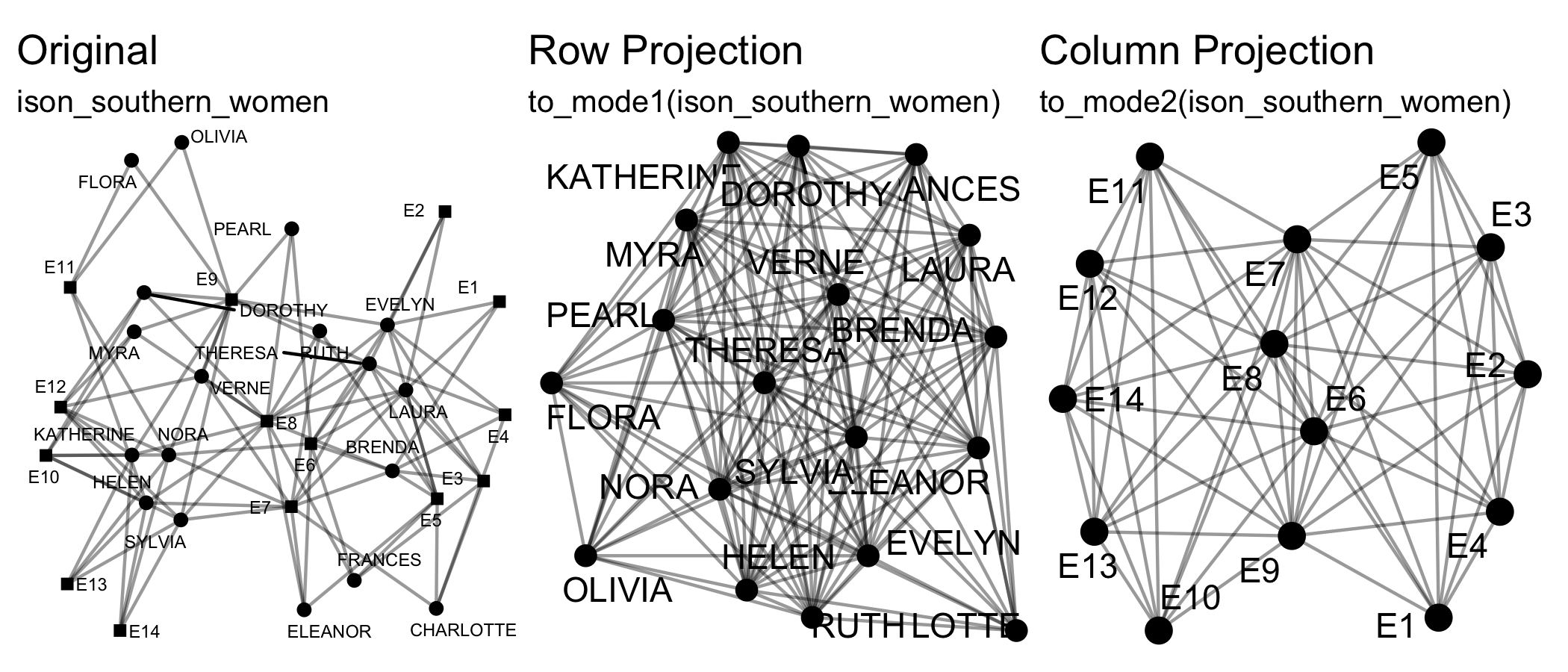
Transforming means changing the dimensions of the network, e.g. from
a two-mode network to a one-mode projection via
to_mode1().
Splitting means separating a network, e.g. from a whole network to
the various ego networks via to_egos().
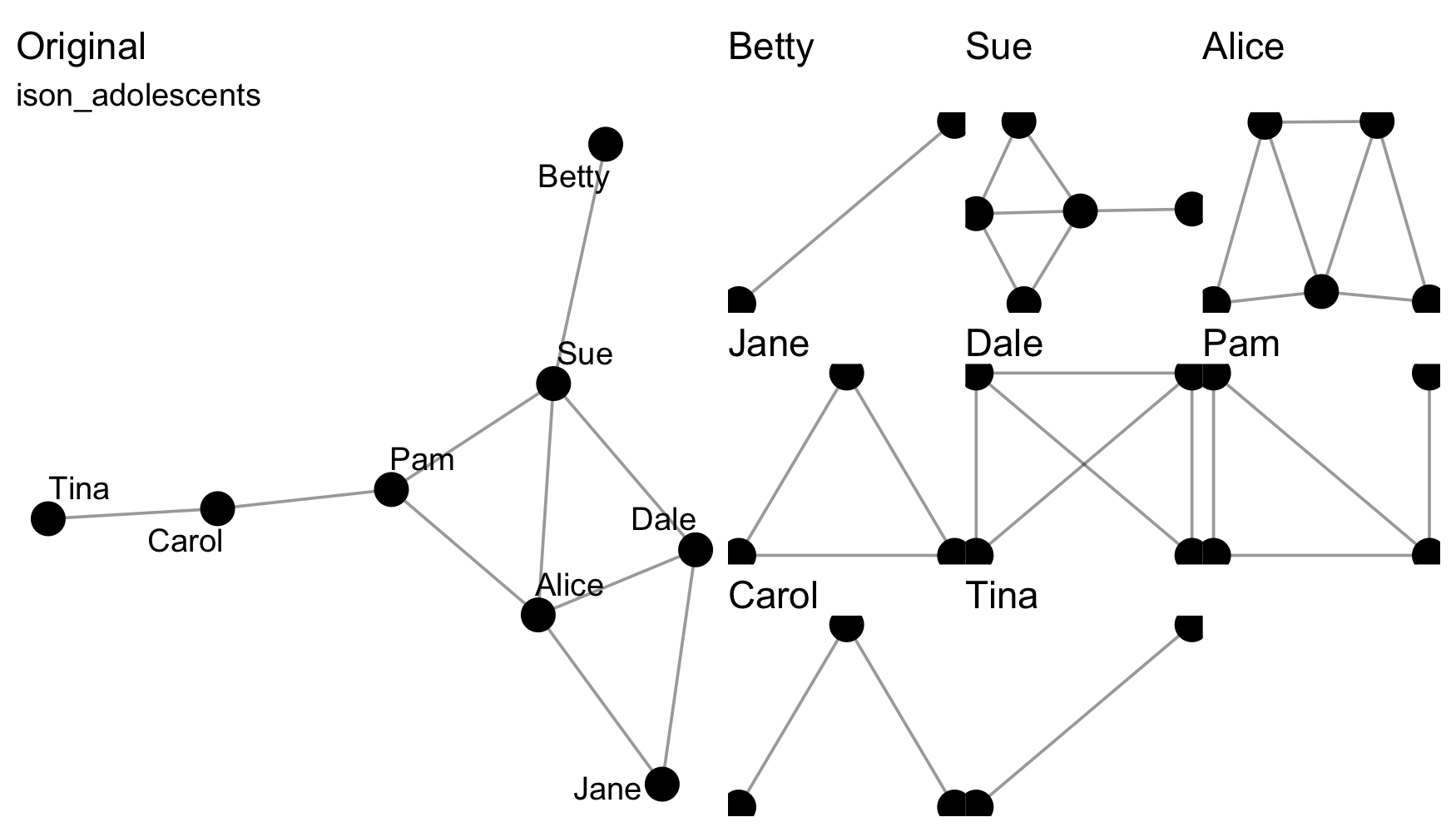
Those functions that split a network into a list of networks are
distinguishable as those to_*() functions that are named in
the plural. Split data can be rejoined using the from_*()
family of functions.
See also to_acyclic(), to_anti(),
to_blocks(), to_components(),
to_correlation(), to_directed(),
to_ego(), to_egos(),
to_eulerian(), to_galois(),
to_giant(), to_matching(),
to_mentoring(), to_mode1(),
to_mode2(), to_multilevel(),
to_named(), to_no_isolates(),
to_onemode(), to_permuted(),
to_reciprocated(), to_redirected(),
to_simplex(), to_slices(),
to_subgraph(), to_subgraphs(),
to_ties(), to_tree(),
to_twomode(), to_undirected(),
to_uniplex(), to_unnamed(),
to_unsigned(), to_unweighted(),
to_waves() and from_egos(),
from_slices(), from_subgraphs(),
from_ties(), from_waves().
{manynet} includes three one-line graphing functions
with sensible defaults based on the network’s properties.
First, graphr() is used to graph networks in any of the
{manynet} formats. It includes sensible defaults so that
researchers can view their network’s structure or distribution quickly
with a minimum of fuss. Compare the output from {manynet}
with a similar default from {igraph}:
Here the {manynet} function recognises that the network
is a two-mode network and uses a bipartite layout by default, and
recognises that the network contains names for the nodes and prints them
vertically so that they are legible in this layout. Other ‘clever’
features include automatic node sizing and more. By contrast,
{igraph} requires the bipartite layout to be specified, has
cumbersome node size defaults for all but the smallest graphs, and
labels also very often need resizing and adjustment to avoid overlap.
All of {manynet}’s adjustments can be overridden,
however…
Changing the size and colors of nodes and ties is as easy as specifying the function’s relevant argument with a replacement, or indicating from which attribute it should inherit this information.
{manynet} can use all the layout algorithms offered by
packages such as {igraph}, {ggraph}, and
{graphlayouts}, and offers some additional layout
algorithms for snapping layouts to a grid, visualising partitions
horizontally, vertically, or concentrically, or conforming to
configurational coordinates.
Lastly, graphr() is highly extensible in terms of the
overall look of your plots. {manynet} uses the excellent
{ggraph} package (and thus {ggplot2}) as a
plotting engine. This enables alterations such as the application of
themes to be applied upon the defaults. If you want to quickly make sure
your plots conform to your institution or taste, then it is easy to do
with themes and scales that update the basic look and color palette used
in your plots.
More themes are on their way, and we’re happy to take suggestions.
Second, graphs() is used to graph multiple networks
together, which can be useful for ego networks or network panels.
{patchwork} is used to help arrange individual plots
together.
Third, grapht() is used to visualise dynamic networks.
It uses {gganimate} and {gifski} to create a
gif that visualises network changes over time. It really couldn’t be
easier.
{manynet} includes four special groups of functions,
each with their own pretty print() and plot()
methods: marks, measures, motifs, and memberships. Marks are logical
scalars or vectors, measures are numeric, memberships categorical, and
motifs result in tabular outputs.
{manynet}’s *is_*() functions offer fast
logical tests of various properties. Whereas is_*() returns
a single logical value for the network, node_is_*() returns
a logical vector the length of the number of nodes in the network, and
tie_is_*() returns a logical vector the length of the
number of ties in the network.
is_acyclic(), is_aperiodic(),
is_attributed(), is_complex(),
is_connected(), is_directed(),
is_dynamic(), is_edgelist(),
is_eulerian(), is_graph(),
is_igraph(), is_labelled(),
is_list(), is_longitudinal(),
is_manynet(), is_multiplex(),
is_perfect_matching(), is_signed(),
is_tidygraph(), is_twomode(),
is_uniplex(), is_weighted()node_is_core(), node_is_cutpoint(),
node_is_exposed(), node_is_fold(),
node_is_independent(), node_is_infected(),
node_is_isolate(), node_is_latent(),
node_is_max(), node_is_mentor(),
node_is_min(), node_is_mode(),
node_is_random(), node_is_recovered()tie_is_bridge(), tie_is_cyclical(),
tie_is_feedback(), tie_is_forbidden(),
tie_is_loop(), tie_is_max(),
tie_is_min(), tie_is_multiple(),
tie_is_path(), tie_is_random(),
tie_is_reciprocated(), tie_is_simmelian(),
tie_is_transitive(), tie_is_triangular(),
tie_is_triplet()The *is_max() and *is_min() functions are
used to identify the maximum or minimum, respectively, node or tie
according to some measure (see below).
{manynet}‘s *by_*() functions tabulate
nodes’ frequency in various motifs. These include:
net_by_brokerage(), net_by_dyad(),
net_by_mixed(), net_by_triad(),
node_by_brokerage(), node_by_exposure(),
node_by_path(), node_by_quad(),
node_by_tie(), node_by_triad(){manynet}‘s *in_*() functions identify
nodes’ membership in some grouping, such as a community or component.
These functions always return a character vector, indicating e.g. that
the first node is a member of group “A”, the second in group “B”,
etc.
node_in_adopter(), node_in_automorphic(),
node_in_betweenness(), node_in_brokering(),
node_in_component(), node_in_eigen(),
node_in_equivalence(), node_in_fluid(),
node_in_greedy(), node_in_infomap(),
node_in_leiden(), node_in_louvain(),
node_in_optimal(), node_in_partition(),
node_in_regular(), node_in_roulette(),
node_in_spinglass(), node_in_strong(),
node_in_structural(), node_in_walktrap(),
node_in_weak()For example node_brokerage_census() returns the
frequency of nodes’ participation in Gould-Fernandez brokerage roles for
a one-mode network, and the Jasny-Lubell brokerage roles for a two-mode
network.
These can be analysed alone, or used as a profile for establishing
equivalence. {manynet} offers both HCA and CONCOR
algorithms, as well as elbow, silhouette, and strict methods for
k-cluster selection.
{manynet} also includes functions for establishing
membership on other bases, such as typical community detection
algorithms, as well as component and core-periphery partitioning
algorithms.
{manynet} also offers a large and growing smorgasbord of
measures that can be used at the node, tie, and network level to measure
some feature, property, or quantity of the network. Each recognises
whether the network is directed or undirected, weighted or unweighted,
one-mode or two-mode. All return normalized values wherever possible,
though this can be overrided. Here are some examples:
node_degree(),
node_closeness(), node_betweenness(), and
node_eigenvector(), net_degree(),
net_closeness(), net_betweenness(), and
net_eigenvector()net_density(),
net_reciprocity(), net_transitivity(),
net_equivalency(), and net_congruency()net_connectedness(),
net_efficiency(), net_upperbound()net_components(),
net_cohesion(), net_adhesion(),
net_diameter(), net_length()node_redundancy(),
node_effsize(), node_efficiency(),
node_constraint(), node_hierarchy()net_richness(),
net_diversity(), net_heterophily(),
net_assortativity(), node_richness(),
node_diversity(), node_heterophily(),
node_assortativity()net_core(),
net_factions(), net_modularity(),
net_smallworld(), net_balance()net_reproduction(),
net_immunity(), node_thresholds()There is a lot here, so we recommend you explore the list of functions to find out more.
This package includes tutorials to help new and experienced users
learn how they can conduct social network analysis using the package.
These tutorials leverage the additional package {learnr}
(see here), but we have
made it easy to use {manynet} or {migraph}
tutorials right out of the box:
run_tute()
#> # A tibble: 9 × 3
#> package name title
#> <chr> <chr> <chr>
#> 1 manynet tutorial0 Intro to R
#> 2 manynet tutorial1 Data
#> 3 manynet tutorial2 Visualisation
#> 4 manynet tutorial3 Centrality
#> 5 manynet tutorial4 Cohesion and Community
#> 6 manynet tutorial5 Position and Equivalence
#> 7 manynet tutorial6 Topology and Resilience
#> 8 manynet tutorial7 Diffusion and Learning
#> 9 migraph tutorial8 Diversity and Regression
# run_tute("tutorial1")The easiest way to install the latest stable version of
{manynet} is via CRAN. Simply open the R console and
enter:
install.packages('manynet')
library(manynet) will then load the package and make the
data and tutorials (see below) contained within the package
available.
For the latest development version, for slightly earlier access to new features or for testing, you may wish to download and install the binaries from Github or install from source locally. The latest binary releases for all major OSes – Windows, Mac, and Linux – can be found here. Download the appropriate binary for your operating system, and install using an adapted version of the following commands:
install.packages("~/Downloads/manynet_winOS.zip", repos = NULL)install.packages("~/Downloads/manynet_macOS.tgz", repos = NULL)install.packages("~/Downloads/manynet_linuxOS.tar.gz", repos = NULL)To install from source the latest main version of
{manynet} from Github, please install the
{remotes} package from CRAN and then:
remotes::install_github("stocnet/manynet")remotes::install_github("stocnet/manynet@develop")Those using Mac computers may also install using Macports:
sudo port install R-manynet
This package stands on the shoulders of several incredible packages.
In terms of the objects it works with, this package aims to provide
an updated, more comprehensive replacement for
{intergraph}. As such it works with objects in
{igraph} and {network} formats, but also
equally well with base matrices and edgelists (data frames), and formats
from several other packages.
The user interface is inspired in some ways by Thomas Lin Pedersen’s
excellent {tidygraph} package, though makes some different
decisions, and uses the quickest {igraph} or
{network} routines where available.
{manynet} has inherited most of its core functionality
from its maternal package, {migraph}.
{migraph} continues to offer more analytic and modelling
functions that builds upon the architecture provided by
{manynet}. For more, please check out
{migraph} directly.
Development on this package has been funded by the Swiss National Science Foundation (SNSF) Grant Number 188976: “Power and Networks and the Rate of Change in Institutional Complexes” (PANARCHIC).
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.