
The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

Markov Random Fields are probabilistic models capable of describing sets of random variables with a local dependence property (the Markov property) defined on a neighborhood system. Particularly on the context of image processing, pixels can be seen as vertices of a graph defined on a finite 2-dimensional lattice, and a neighborhood system can be defined based on their relative positions to construct a MRF.

The goal of mrf2d is to provide a framework for the
analysis of Markov Random Fields with pairwise interactions on
2-dimensional lattices, including Hidden Markov Random Fields. It
introduces the S4 class mrfi to describe interaction
structures in a very general way, being able to adapt from very simple
cases like the Ising Model to complex anisotropic models with different
types of interaction.


A complete paper describing the details of the package and examples is published in the Journal of Statistical Software and can be found here.
You can install the stable version of mrf2d from CRAN with:
install.packages("mrf2d")The development version is available on the package’s Github page. It can be
installed with the devtools package by using
devtools::install_github("Freguglia/mrf2d")mrf2d introduces a programming interface for the general
Markov Random Field model in Freguglia, Victor, Nancy L. Garcia, and
Juliano L. Bicas. “Hidden Markov random field models applied to color
homogeneity evaluation in dyed textile images.” Environmetrics (2019):
e2613. Using specific interaction structures and parameter
restrictions can lead to important models as particular cases, such as
the Potts model.
It introduces the S4 class mrfi to represent interaction
structures. The mrfi() function can be used to create these
objects representing interaction structures with relative positions
included based on the norm of the relative position (distance) or
explicitly specified
interact <- mrfi(max_norm = 1, positions = list(c(4,2)))
interact
#> 3 interacting positions.
#> rx ry
#> 1 0
#> 0 1
#> 4 2
plot(interact)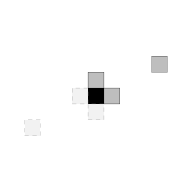
Potentials (parameters) are represented by three-dimensional arrays, where rows and columns represent pixel label values and slices represent interacting positions.
potentials <- expand_array(c(-0.9, -0.9, 0.2), family = "oneeach", C = 1, mrfi = interact)
potentials
#> , , (1,0)
#>
#> 0 1
#> 0 0.0 -0.9
#> 1 -0.9 0.0
#>
#> , , (0,1)
#>
#> 0 1
#> 0 0.0 -0.9
#> 1 -0.9 0.0
#>
#> , , (4,2)
#>
#> 0 1
#> 0 0.0 0.2
#> 1 0.2 0.0The negative values out of diagonal means different “colors” are less likely in that relative position.
The package has many built-in functions for sampling, potentials estimation and hidden MRF model fitting (used for image segmentation), but it also provides all the basic stack of computations used to implement algorithms for MRF models, making it suitable for development of research in Markov Random Field models.
set.seed(1)
img_dim <- c(200,200)
Z <- rmrf2d(img_dim, mrfi = interact, theta = potentials, cycles = 60)
dplot(Z, legend = TRUE)
If you’re interested in contributing or found a bug or error, please file an issue. Contributions can be done in form of code optimization, new ideas, discussing new structures, etc.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.