The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

nexus

R-CMD-check codecov CodeFactor Dependencies

r-universe CRAN Version CRAN checks CRAN Downloads

Project Status: WIP – Initial development is in progress, but there has not yet been a stable, usable release suitable for the public.

DOI

Overview

This package is currently experimental. This means that it is functional, but interfaces and functionalities may change over time, testing and documentation may be lacking.

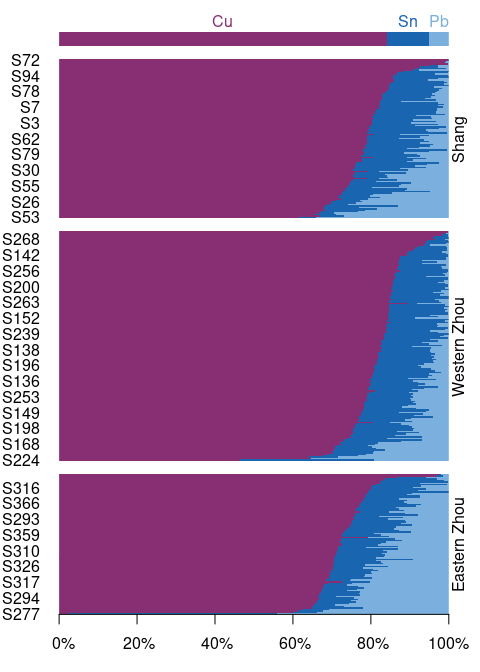
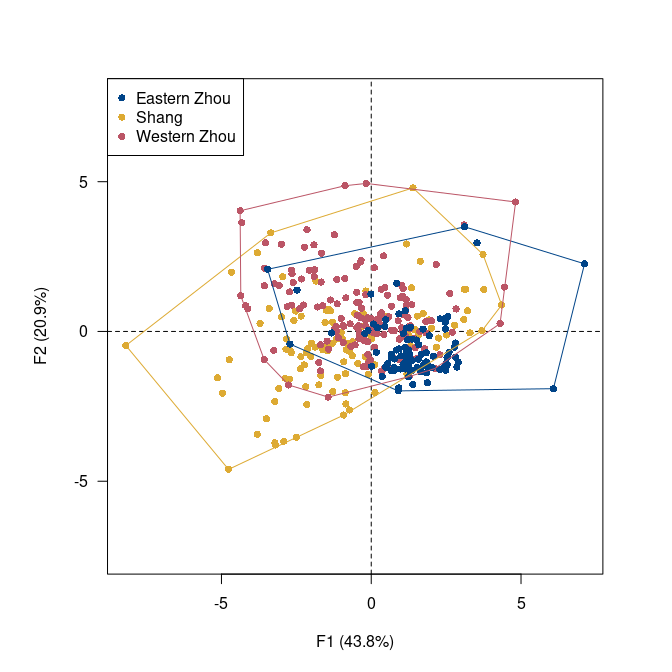
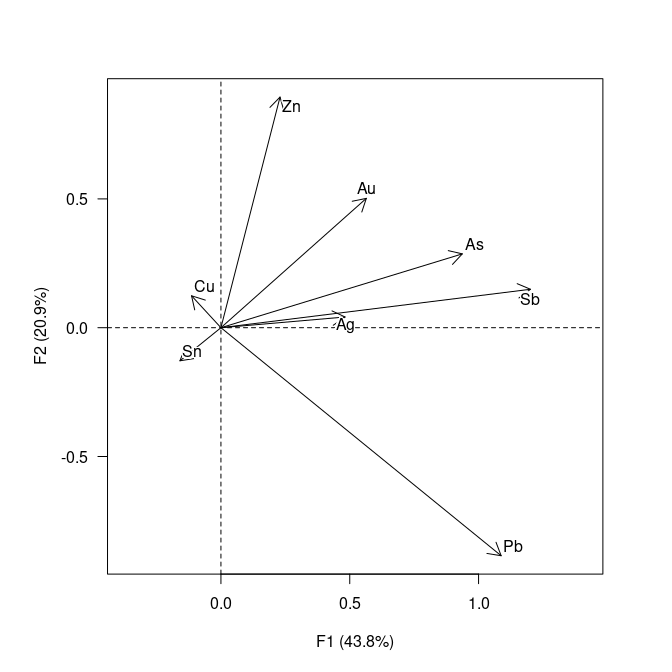
Exploration and analysis of compositional data in the framework of J. Aitchison (1986). nexus provides tools for chemical fingerprinting and source tracking of ancient materials. This package provides methods for compositional data analysis:

This package also includes methods for provenance studies:

isopleuros is a companion package to nexus that allows to create ternary plots.

To cite nexus in publications use:

Frerebeau N, Philippe A (2024). nexus: Sourcing Archaeological Materials by Chemical Composition. Université Bordeaux Montaigne, Pessac, France. doi:10.5281/zenodo.10225630 https://doi.org/10.5281/zenodo.10225630, R package version 0.3.0, https://packages.tesselle.org/nexus/.

This package is a part of the tesselle project https://www.tesselle.org.

Installation

You can install the released version of nexus from CRAN with:

install.packages("nexus")

And the development version from GitHub with:

# install.packages("remotes")
remotes::install_github("tesselle/nexus")

Usage

## Install extra packages (if needed)
# install.packages("folio")

## Load the package
library(nexus)
#> Loading required package: dimensio

nexus provides a set of S4 classes that represent different special types of matrix (see vignette("nexus")). The most basic class represents a compositional data matrix, i.e. quantitative (nonnegative) descriptions of the parts of some whole, carrying relative, rather than absolute, information (J. Aitchison 1986).

It assumes that you keep your data tidy: each variable must be saved in its own column and each observation (sample) must be saved in its own row.

## Data from Wood and Liu 2023
data("bronze", package = "folio")

## Coerce to compositional data
coda <- as_composition(bronze, parts = 4:11)

## Use dynasties as groups
groups(coda) <- bronze$dynasty
## Compositional barplots of major elements
barplot(coda, select = is_element_major(coda), order_rows = "Cu",
        border = NA, space = 0)

## Log-ratio analysis
## (PCA of centered log-ratio; outliers should be removed first)
clr <- transform_clr(coda, weights = TRUE)
lra <- pca(clr)

## Visualize results
viz_individuals(lra, color = c("#004488", "#DDAA33", "#BB5566"))
viz_hull(x = lra, border = c("#004488", "#DDAA33", "#BB5566"))

viz_variables(lra)

Contributing

Please note that the nexus project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.

References

Aitchison, J. 1986. The Statistical Analysis of Compositional Data. Monographs on Statistics and Applied Probability. Londres, UK ; New York, USA: Chapman and Hall.
———. 1997. “The One-Hour Course in Compositional Data Analysis or Compositional Data Analysis Is Simple.” In IAMG’97, edited by V. Pawlowsky-Glahn, 3–35. Barcelona: International Center for Numerical Methods in Engineering (CIMNE).
Aitchison, John, and Michael Greenacre. 2002. “Biplots of Compositional Data.” Journal of the Royal Statistical Society: Series C (Applied Statistics) 51 (4): 375–92. https://doi.org/10.1111/1467-9876.00275.
Baxter, M. J., C. C. Beardah, I. Papageorgiou, M. A. Cau, P. M. Day, and V. Kilikoglou. 2008. “On Statistical Approaches to the Study of Ceramic Artefacts Using Geochemical and Petrographic Data.” Archaeometry 50 (1): 142–57. https://doi.org/10.1111/j.1475-4754.2007.00359.x.
Beardah, C. C., M. J. Baxter, I. Papageorgiou, and M. A. Cau. 2003. ““Mixed-mode” Approaches to the Grouping of Ceramic Artefacts Using S-Plus.” In The Digital Heritage of Archaeology., edited by M. Doerr and A. Sarris, 261–66. Athens: Archive of Monuments and Publications, Hellenic Ministry of Culture.
Boogaart, K. Gerald van den, and Raimon Tolosana-Delgado. 2013. Analyzing Compositional Data with R. Use R! Berlin Heidelberg: Springer-Verlag. https://doi.org/10.1007/978-3-642-36809-7.
Cau, Miguel-Angel, Peter M Day, Michael J Baxter, Ioulia Papageorgiou, Ioannis Iliopoulos, and Giuseppe Montana. 2004. “Exploring Automatic Grouping Procedures in Ceramic Petrology.” Journal of Archaeological Science 31 (9): 1325–38. https://doi.org/10.1016/j.jas.2004.03.006.
Egozcue, J. J., V. Pawlowsky-Glahn, G. Mateu-Figueras, and C. Barceló-Vidal. 2003. “Isometric Logratio Transformations for Compositional Data Analysis.” Mathematical Geology 35 (3): 279–300. https://doi.org/10.1023/A:1023818214614.
Egozcue, Juan José, Caterina Gozzi, Antonella Buccianti, and Vera Pawlowsky-Glahn. 2024. “Exploring Geochemical Data Using Compositional Techniques: A Practical Guide.” Journal of Geochemical Exploration 258 (March): 107385. https://doi.org/10.1016/j.gexplo.2024.107385.
Egozcue, Juan José, and Vera Pawlowsky-Glahn. 2023. “Subcompositional Coherence and and a Novel Proportionality Index of Parts.” SORT 47 (2): 229–44. https://doi.org/10.57645/20.8080.02.7.
Filzmoser, Peter, Robert G. Garrett, and Clemens Reimann. 2005. “Multivariate Outlier Detection in Exploration Geochemistry.” Computers & Geosciences 31 (5): 579–87. https://doi.org/10.1016/j.cageo.2004.11.013.
Filzmoser, Peter, and Karel Hron. 2008. “Outlier Detection for Compositional Data Using Robust Methods.” Mathematical Geosciences 40 (3): 233–48. https://doi.org/10.1007/s11004-007-9141-5.
Filzmoser, Peter, Karel Hron, and Clemens Reimann. 2009a. “Principal Component Analysis for Compositional Data with Outliers.” Environmetrics 20 (6): 621–32. https://doi.org/10.1002/env.966.
———. 2009b. “Univariate Statistical Analysis of Environmental (Compositional) Data: Problems and Possibilities.” Science of The Total Environment 407 (23): 6100–6108. https://doi.org/10.1016/j.scitotenv.2009.08.008.
———. 2010. “The Bivariate Statistical Analysis of Environmental (Compositional) Data.” Science of The Total Environment 408 (19): 4230–38. https://doi.org/10.1016/j.scitotenv.2010.05.011.
———. 2012. “Interpretation of Multivariate Outliers for Compositional Data.” Computers & Geosciences 39: 77–85. https://doi.org/10.1016/j.cageo.2011.06.014.
Filzmoser, Peter, Karel Hron, and Matthias Templ. 2018. Applied Compositional Data Analysis: With Worked Examples in R. Use R! Berlin Heidelberg: Springer-Verlag. https://doi.org/10.1007/978-3-319-96422-5.
Fišerová, Eva, and Karel Hron. 2011. “On the Interpretation of Orthonormal Coordinates for Compositional Data.” Mathematical Geosciences 43 (4): 455–68. https://doi.org/10.1007/s11004-011-9333-x.
Greenacre, Michael. 2021. “Compositional Data Analysis.” Annual Review of Statistics and Its Application 8 (1): 271–99. https://doi.org/10.1146/annurev-statistics-042720-124436.
Greenacre, Michael J. 2019. Compositional Data Analysis in Practice. Chapman & Hall/CRC Interdisciplinary Statistics. Boca Raton: CRC Press, Taylor & Francis Group.
Grunsky, Eric, Michael Greenacre, and Bruce Kjarsgaard. 2024. “GeoCoDA: Recognizing and Validating Structural Processes in Geochemical Data. A Workflow on Compositional Data Analysis in Lithogeochemistry.” Applied Computing and Geosciences 22 (June): 100149. https://doi.org/10.1016/j.acags.2023.100149.
Hron, Karel, Peter Filzmoser, Patrice de Caritat, Eva Fišerová, and Alžběta Gardlo. 2017. “Weighted Pivot Coordinates for Compositional Data and Their Application to Geochemical Mapping.” Mathematical Geosciences 49 (6): 797–814. https://doi.org/10.1007/s11004-017-9684-z.
Hron, Karel, and Lubomír Kubáček. 2011. “Statistical Properties of the Total Variation Estimator for Compositional Data.” Metrika 74 (2): 221–30. https://doi.org/10.1007/s00184-010-0299-3.
Hron, K., M. Templ, and P. Filzmoser. 2010. “Imputation of Missing Values for Compositional Data Using Classical and Robust Methods.” Computational Statistics & Data Analysis 54 (12): 3095–3107. https://doi.org/10.1016/j.csda.2009.11.023.
Martín-Fernández, J. A., C. Barceló-Vidal, and V. Pawlowsky-Glahn. 2003. “Dealing with Zeros and Missing Values in Compositional Data Sets Using Nonparametric Imputation.” Mathematical Geology 35 (3): 253–78. https://doi.org/10.1023/A:1023866030544.
Pawlowsky-Glahn, V., and J. J. Egozcue. 2001. “Geometric Approach to Statistical Analysis on the Simplex.” Stochastic Environmental Research and Risk Assessment 15 (5): 384–98. https://doi.org/10.1007/s004770100077.
Rousseeuw, Peter J., and Bert C. van Zomeren. 1990. “Unmasking Multivariate Outliers and Leverage Points.” Journal of the American Statistical Association 85 (411): 633–39. https://doi.org/10.1080/01621459.1990.10474920.
Santos, Frédéric. 2020. “Modern Methods for Old Data: An Overview of Some Robust Methods for Outliers Detection with Applications in Osteology.” Journal of Archaeological Science: Reports 32: 102423. https://doi.org/10.1016/j.jasrep.2020.102423.
Weigand, P. C., G. Harbottle, and E. Sayre. 1977. “Turquoise Sources and Source Analysisis: Mesoamerica and the Southwestern U.S.A.” In Exchange Systems in Prehistory, edited by J. Ericson and T. K. Earle, 15–34. New York, NY: Academic Press.

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.