The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
The goal of pedbuildr is to reconstruct pedigrees from genotype data. This is done by optimising the likelihood over all possible pedigrees subject to given restrictions. As part of the pedsuite ecosystem of R packages for pedigree analysis, it uses pedtools for handling pedigrees, and imports pedprobr for calculating pedigree likelihoods.
See also the ibdEstimate() function of forrel, which does
pairwise relatedness estimation.
The pedbuildr package can be installed from CRAN as follows:
install.packages("pedbuildr")Alternatively, the latest development version is available from GitHub.
# install.packages("devtools")
devtools::install_github("magnusdv/pedbuildr")To get started, load pedbuildr.
library(pedbuildr)
#> Loading required package: pedtoolsThe built-in dataset trioData contains simulated
genotypes for three individuals at 100 equifrequent SNP markers. Here
are the first 10 columns:
trioData[, 1:10]
#> <1> <2> <3> <4> <5> <6> <7> <8> <9> <10>
#> 1 "1/2" "1/2" "1/1" "1/2" "1/2" "1/2" "1/2" "2/2" "1/2" "1/2"
#> 2 "1/1" "1/2" "1/2" "2/2" "1/2" "2/2" "1/2" "2/2" "1/2" "2/2"
#> 3 "1/1" "1/2" "1/2" "2/2" "1/1" "1/2" "1/2" "1/2" "1/2" "2/2"As a simple demonstration we will try to reconstruct the pedigree
connecting these individuals assuming they are all males. To initialise
the process we create them as singletons and attach the marker data. The
locusAttributes argument tells R that all the markers are
diallelic with alleles 1 and 2.
x = list(singleton(1),
singleton(2),
singleton(3)) |>
setMarkers(alleleMatrix = trioData, locusAttributes = "snp12")
plotPedList(x, frames = FALSE)
To reconstruct the pedigree, simply run
reconstruct():
res = reconstruct(x)
#> Pedigree parameters:
#> ID labels: 1, 2, 3
#> Sex: 1, 1, 1
#> Extra: parents
#> Age info: -
#> Known PO: -
#> Known non-PO: -
#> No children: -
#> Connected only: TRUE
#> Symmetry filter: TRUE
#> Max inbreeding: 0.0625
#> Linear inbreeding: FALSE
#>
#> Building pedigree list:
#> Undirected adjacency matrices: 8
#> Directed adjacency matrices: 16
#> After adding parents: 57
#> Connected solutions: 44
#> Excessive inbreeding: 0
#>
#> Computing the likelihood of 44 pedigrees.
#> Sorting by descending likelihood.
#> Total time used: 1.6 secsA tailor-made plot function makes it easy to visualise
the most likely pedigrees:
plot(res, top = 6)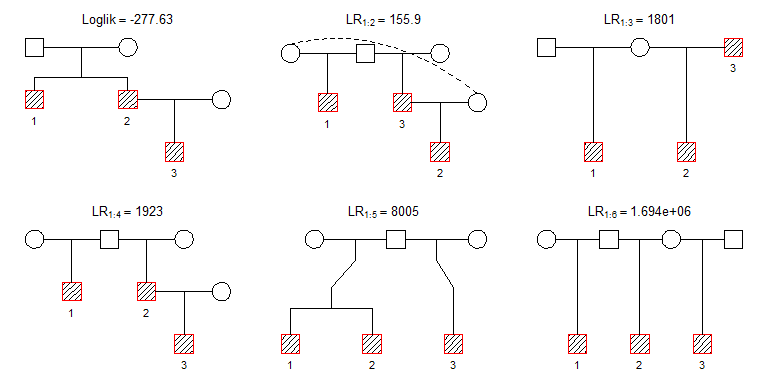
The most likely pedigree is plotted top left. The titles for the remaining pedigrees give the likelihood ratio (LR) comparing the first pedigree to the one shown. For example, the first solution is 155.9 more likely than the second.
A priori there are infinitely many possible pedigrees
connecting a set of individuals. (For example, two individuals may be
k’th cousins for any k = 1,2,… .) In order to obtain a
manageable search space, reconstruct() offers a range of
restriction parameters:
extra: The number of extra individuals allowed to
connect the original individuals. (See further explanations below.)age: A vector of numeric (relative) ages or age
inequalities. For example,
age = c("A > B,C", "B > D") excludes B and C as
ancestors of A, and D as an ancestor of B (but no assumption is made for
C vs. D).inferPO: When this is TRUE, an initial
pairwise estimation step is done to infer high-confidence parent/child
pairs, and also non-parent/child pairs.knownPO: Known parent–offspring pairs. Note that these
are unordered pairs, i.e., with no assumption on who is the
parent and who is the child. (If this is known, use age to
indicate it.)notPO: Pairs known not to be parent–offspring.allKnown: If TRUE, then knownPO is taken
to be the complete list of parent–offspring pairs.noChildren: Individuals known to have no children.maxInbreeding: The highest permitted inbreeding
coefficient in the pedigree. By default this is set to 1/16, which is
appropriate for most projects involving human pedigrees.linearInb: The allowed level of inbreeding between
linear descendants. For example, linearInb = 1 allows
mating between parent–child, but not grandparent–grandchild. The default
value FALSE disallows all inbreeding of this type.connected: If TRUE (default), only connected pedigrees
are considered.sexSymmetry: If TRUE (default) pedigrees are considered
equal if they differ only in the sexes of the added parents, e.g.,
paternal versus maternal half-siblings.Let us re-run the reconstruction of trioData adding a
few of these restrictions. We allow 3 extra individuals and indicate
that individual 1 is older than the others. Furthermore, we ask the
program to infer parent-child relationships automatically. Finally we
allow any amount of inbreeding.
res2 = reconstruct(x, extra = 3, age = "1 > 2,3", inferPO = TRUE, maxInbreeding = 1)
#> Pairwise estimation:
#> PO: 2-3
#> non-PO: 1-3
#>
#> Pedigree parameters:
#> ID labels: 1, 2, 3
#> Sex: 1, 1, 1
#> Extra: 3
#> Age info: 1>2, 1>3
#> Known PO: 2-3
#> Known non-PO: 1-3
#> No children: -
#> Connected only: TRUE
#> Symmetry filter: TRUE
#> Max inbreeding: 1
#> Linear inbreeding: FALSE
#>
#> Building pedigree list:
#> First 2: 2 candidates (0.0027 secs)
#> All 3 + 0 extra: 1 solutions | 3 candidates (0.00353 secs)
#> All 3 + 1 extra: 9 solutions | 30 candidates | 21 duplicates removed (0.0491 secs)
#> All 3 + 2 extra: 35 solutions | 266 candidates | 501 duplicates removed (0.221 secs)
#> All 3 + 3 extra: 183 solutions | 183 candidates | 459 duplicates removed (0.842 secs)
#> Total solutions: 228
#> Converting to ped
#> Excessive inbreeding: 0
#> Time used: 1.07 secs
#>
#> Computing the likelihood of 228 pedigrees.
#> Sorting by descending likelihood.
#> Total time used: 18.1 secsThe most likely results this time are shown below:
plot(res2, top = 6)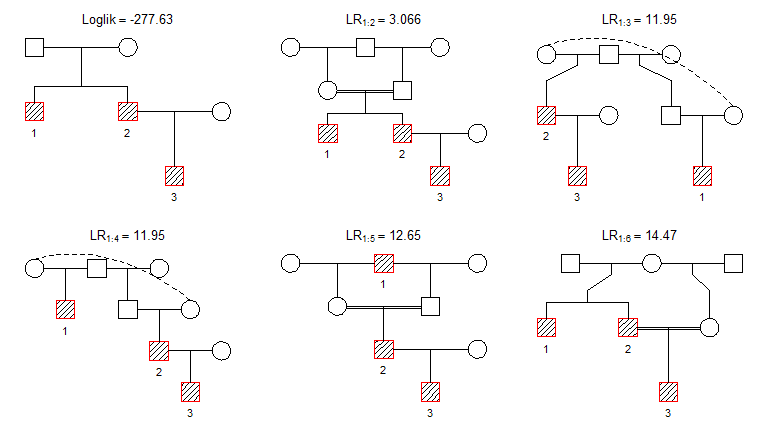
We see that the same pedigree “wins”, but some inbred/esoteric alternatives have appeared among the runners-up.
extraArguably the most important parameter to reconstruct()
is extra, which controls the size of the pedigrees to
consider. It can be either a nonnegative integer, or the word “parents”.
If an integer, it sets the maximum number of extra members used to
connect the original individuals. (The final pedigrees may contain
further extras still, since missing parents are added at the end.)
If extra = "parents", a special algorithm is invoked.
First all directed acyclic graphs between the original individuals are
generated, and then parents are added in all possible ways. This is
(currently) the default behaviour, since it avoids setting an ad
hoc number of “extras”. However, it only works well in relatively
small cases.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.