The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
The r2mlm package contains functions that compute a framework of total and level-specific R-squared measures for multilevel models, with accompanying plots; these plots allow interpreting and visualizing all of the measures together as an integrated set. The framework of R-squared measures subsumes and analytically relates 10 previously-developed measures as special cases of 5 measures from this framework, as well as provides several new measures. The framework is presented in Rights & Sterba (2019) for evaluating a single fitted multilevel model. The implementation of this framework of measures for comparing multilevel models using R-squared differences is described in Rights & Sterba (2020). The functions in this package allow users to input either model objects obtained from lme4 or nlme, or to manually input model parameter estimates.
You can install the released version of r2mlm from CRAN with:
And the development version from GitHub with:
Suppose you have a dataset consisting of teachers nested within schools. A researcher could specify a multilevel model with teacher job satisfaction as the outcome, which is predicted by the level-1 predictor teacher salary (here school-mean-centered) and the level-2 predictor student-teacher ratio. Suppose the multilevel model included a random intercept as well as a random slope of teacher salary, and included normally-distributed, homoscedastic level-1 residuals. The researcher could then obtain the following output (see r2mlm function for further details).
library(r2mlm)
#> Loading required package: lme4
#> Loading required package: Matrix
#> Loading required package: nlme
#>
#> Attaching package: 'nlme'
#> The following object is masked from 'package:lme4':
#>
#> lmList
# Generate the model, in this case with lme4:
model <- lmer(satisfaction ~ 1 + salary_c + s_t_ratio + (1 + salary_c | schoolID), data = teachsat, REML = TRUE)
#> Warning in checkConv(attr(opt, "derivs"), opt$par, ctrl = control$checkConv, :
#> Model failed to converge with max|grad| = 0.00626324 (tol = 0.002, component 1)
# Adjust plot margins
par(mar = c(6.75, 10.5, 2.625, 10.5))
# Generate R-squared measures for that model:
r2mlm(model)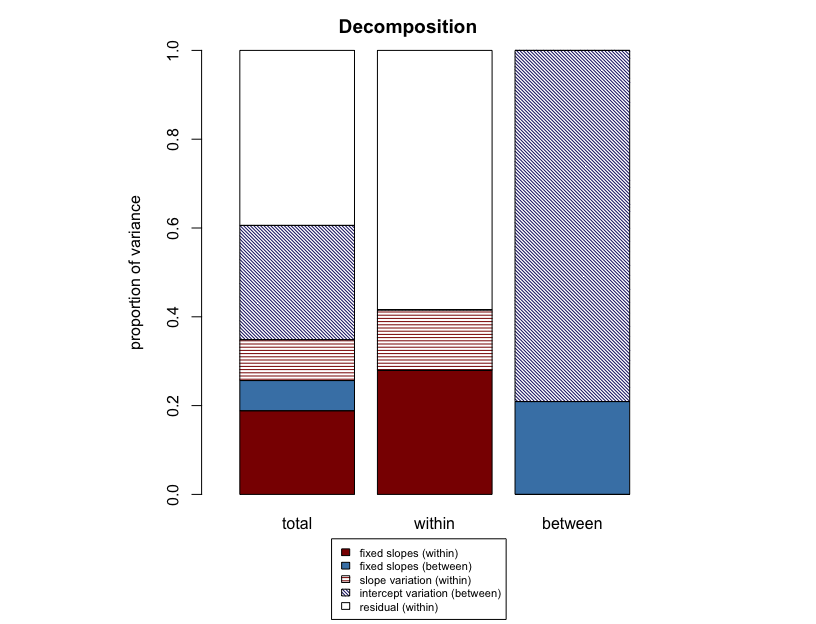
#> $Decompositions
#> total within between
#> fixed, within 0.18837930 0.2792572 NA
#> fixed, between 0.06806328 NA 0.2091505
#> slope variation 0.09206018 0.1364718 NA
#> mean variation 0.25736400 NA 0.7908495
#> sigma2 0.39413323 0.5842709 NA
#>
#> $R2s
#> total within between
#> f1 0.18837930 0.2792572 NA
#> f2 0.06806328 NA 0.2091505
#> v 0.09206018 0.1364718 NA
#> m 0.25736400 NA 0.7908495
#> f 0.25644258 NA NA
#> fv 0.34850277 0.4157291 NA
#> fvm 0.60586677 NA NAThere are two main functions currently available in r2mlm:
r2mlm(), for computing variance explained for a single multilevel model.r2mlm_comp(), for comparing variance explained between two different multilevel models.In some cases, you might run a multilevel model that will not converge in nlme or lme4, but will converge in another software package (e.g., HLM, Mplus). If you run your model and obtain the associated output, you can manually generate R-squared measures using r2mlm_manual() or r2mlm_comp_manual(). For manual entry details, see the help pages:
This framework of variance explained assumes the following:
Rights, J. D., & Sterba, S. K. (2019). Quantifying explained variance in multilevel models: An integrative framework for defining R-squared measures. Psychological Methods, 24(3), 309–338. https://doi.org/10.1037/met0000184
Rights, J. D., & Sterba, S. K. (2020). New recommendations on the use of R-squared differences in multilevel model comparisons. Multivariate Behavioral Research. https://doi.org/10.1080/00273171.2019.1660605
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.