The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

revpref

Travis build status

The goal of revpref is to provide a set of tools to (i) check consistency of a finite set of consumer demand observations with a number of revealed preference axioms at a given efficiency level, (ii) compute goodness-of-fit indices when the data do not obey the axioms, and (iii) compute power against uniformly random behavior. Below we provide a brief description of the functions provided in this package.

Installation

You can install the released version of revpref from CRAN with:

install.packages("revpref")

And the development version from GitHub with:

# install.packages("devtools")
devtools::install_github("ksurana21/revpref")

Example

Below we provide some simple examples to illustrate the three types of functionality available within the package. To begin with, we define the price and quantity matrices. Both of these matrices (defined below) have ten rows corresponding to the number of observations and three columns corresponding to the number of consumption categories.


# Load the package
library(revpref)

# Define a price matrix 
p = matrix(c(4, 4, 4, 1, 9, 3, 2, 8, 3, 1, 
             8, 4, 3, 1, 9, 3, 2, 8, 8, 4,
             1, 4, 1, 8, 9, 3, 1, 8, 3, 2),
           nrow = 10, ncol = 3, byrow = TRUE)

# Define a quantity matrix
q = matrix(c( 01.81, 00.19, 10.51, 17.28, 02.26, 04.13, 12.33, 02.05, 02.99, 06.06,
              05.19, 00.62, 11.34, 10.33, 00.63, 04.33, 08.08, 02.61, 04.36, 01.34,
              09.76, 01.37, 36.35, 01.02, 03.21, 04.97, 06.20, 00.32, 08.53, 10.92),
           nrow = 10, ncol = 3, byrow = TRUE)

Nonparametric tests

First, we check whether the data violate the rationality axioms. We begin with GARP.


# Test consistency with GARP and compute the number of GARP violations
result <- garp(p, q)
result
#> [1] 0 8

The first output is a binary indicator telling us whether the data set passed the GARP test. Here, we see that the first output is 0 which means that the data set is inconsistent with GARP. The second output indicates that there are 8 GARP violations. In this example, we did not specify the efficiency level, in which case the default value of 1 was applied. In the next example, we check GARP at the efficiency level e = 0.90.


# Test consistency with GARP and compute the number of violations at the efficiency level 0.90
result <- garp(p, q, efficiency = 0.90)
result
#> [1] 1 0

Here we see that the first output is 1 which means that the data set is consistent with GARP at the efficiency level e = 0.90. As expected, the second output is 0 indicating that there are no GARP violations at this efficiency level. Next, we follow similar procedures to test consistency with SARP and WARP at full efficiency.


# Test consistency with SARP and compute the number of SARP violations
result <- sarp(p, q)
result 
#> [1] 0 8

# Test consistency with WARP and compute the number of WARP violations
result <- warp(p, q)
result 
#> [1] 0 1

We see that the data set is inconsistent with both SARP and WARP. All the three tests revealed that our data set failed to satisfy the rationality axioms. However, these tests did not indicate how close this set of observations is to satisfying the exact axioms. In the next step, we compute goodness-of-fit indices to measure the severity of violations.

Goodness-of-fit

The package provides functionalities for two goodness-of-fit measures. The first measure is the critical cost efficiency index (CCEI) which is defined as the maximal efficiency level at which the data set is consistent with the rationality axiom(s). From the previous exercises, we know that our data set failed to satisfy GARP at full efficiency but is consistent with GARP at the efficiency level 0.90. As such, we expect the CCEI to be greater than 0.90 but less than 1.


# Compute the Critical Cost Efficiency Index (CCEI)
result <- ccei(p, q)
result
#> [1] 0.9488409

Using the function ccei, we find that the highest efficiency level at which the data set is consistent with GARP is equal to 0.9488. This indicates that although our data set is inconsistent with the exact GARP, it is very close to satisfying it. We can also compute the CCEI for SARP and WARP by providing an additional argument (model = “SARP” or model = “WARP”).


# Compute the Critical Cost Efficiency Index (CCEI) for SARP
result <- ccei(p, q, model = "SARP")
result
#> [1] 0.9488409

The second goodness-of-fit measure which can be computed through this package is the money pump index (MPI). We can compute the minimum and maximum MPI using the function mpi as follows,


# Compute the minimum and maximum Money Pump Index (MPI)
result <- mpi(p, q)
result
#> [1] 0.07242757 0.18732824

The output tells us that the minimum and maximum MPIs for this data set are 0.07243 and 0.1873, respectively. This means that the consumer is losing 7.24% of the budget in the least severe violation and 18.73% of the budget in the most severe violation. Implicitly, these values provide a bound on the amounts of money that can be pumped from this consumer.

Power

In addition to goodness-of-fit measures, empirical studies usually also report the power measure. As discussed above, the power of a revealed preference test is a measure of the likelihood of detecting an irrational behavior. We can use the function bronars to compute the Bronars power index for the given data set.


# Compute power 
result <- bronars(p, q)
result
#> [1] 0.839

We find that for the given budget conditions, there is about 83.90% probability of detecting irrational behavior. As discussed above, here we have followed Becker’s (1962) approach of using uniformly random consumption choices to simulate irrational consumers. As a final exercise, we analyze how the power of the GARP test changes with the efficiency level.


# Compute power of the GARP test at efficiency levels between 0.4 to 1
power <- c()
for(i in seq(0.4, 1, by = 0.05)){
  power = rbind(power, c(i, bronars(p, q, model = "GARP", simulation = 1000, 
                                    efficiency = i)))
}

# Plot the power measures against efficiency levels
power <- as.data.frame(power)
names(power) <- c("efficiency", "power")
plot(power, type = "b",col = "black", lwd = 1, pch = 20, bty = "L")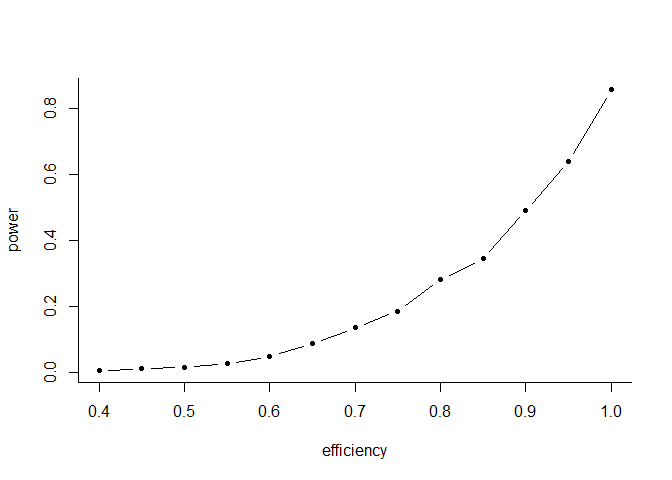

As depicted in the figure above, the power of the GARP test increases with the efficiency level. This is expected as the lower is the efficiency level, the weaker is the test. In other words, with lower values of efficiency, a larger fraction of the simulated data is able to pass the test and hence the probability of rejecting GARP is smaller.

References

These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.