
The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

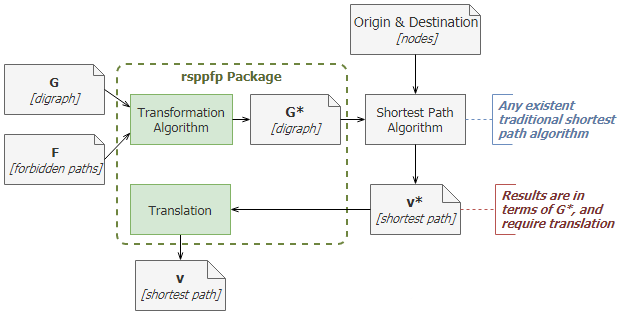
The rsppfp package implements different algorithms for transforming graphs in the Shortest Path Problem with Forbidden Paths (SPPFP). This problem is an important concept in the field of graph theories, and it is a variant of the traditional shortest path problem. In here, there is an additional constrait that takes the form of a finite set of forbidden paths (arc sequences of at least three nodes) that cannot be part of any solution path.
This problem is solved by transforming the original graph
G and its set of forbidden paths F, generating
a new graph G* in which traditional shortest path
algorithms can be applied, and obtain solutions that abide to the
restrictions. This approach has a number of advantages:
G* with algorithms that efficiently manage time and
processing resources constraints, having been implemented in a plethora
of languages.G* is highly compatible with existing
libraries, and can be used as input data for other, more complex
problems and researches.G and F
remain unchanged for long periods of time. Thus, the transformation is
completed only once, and G* can be stored along with the
original graph. A new conversion is required only on the rare cases
where the graph, or its forbidden paths, are modified.This solving process is illustrated in Figure 1, using a paper notation to indicate input and output data. Even more, rsppfp scope and key functionalities are also highlighted.
rsppfp implements two different algorithms, each one suited for different situations:
F must be known beforehand. This
transformation is slightly fast, but generates bigger graphs
G*. Each forbidden path can be of different size, but no
sub-path (of at least three nodes long) can be part of another forbidden
path.G*, by adding less new nodes and arcs. However, this
algorithm is slightly slower.Both algorithms are analyzed using 27 graphs, randomly generated. The complete benchmark evaluation can be found here.
As from 2018-11-22 you can install rsppfp directly from CRAN, using:
{r cran-install, eval = FALSE} install.packages("rsppfp")
You can also install the development version of rsppfp from GitHub with:
{r gh-installation, eval = FALSE} # install.packages("devtools") devtools::install_github("melvidoni/rsppfp")
Available at References
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.