The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.
sparseR:
Sift smartly through interactions & polynomials with ranked
sparsityThe ranked sparsity methods such as the sparsity-ranked lasso (SRL) have been developed for model selection and estimation in the presence of interactions and polynomials (Peterson & Cavanaugh 2022)[https://doi.org/10.1007/s10182-021-00431-7]. The main idea is that an algorithm should be more skeptical of higher-order polynomials and interactions a priori compared to main effects, by a predetermined amount.
The sparseR package has many features designed to
streamline sifting through the high-dimensional space of interaction
terms and polynomials, including functions for variable pre-processing,
variable selection, post-selection inference, and post-fit model
visualization under ranked sparsity. The package implements
ranked-sparsity-based versions of the lasso, elastic net, MCP, and SCAD.
We also provide a (preliminary) version of an sparsity-ranked extension
to Bayesian Information Criterion (and corresponding stepwise
approaches).
## Via GitHub:
# install.packages("devtools")
devtools::install_github("petersonR/sparseR")
# or via CRAN
install.packages("sparseR")library(sparseR)data(iris)
srl <- sparseR(Sepal.Width ~ ., data = iris, k = 1, poly = 2, seed = 1)
srl
#>
#> Model summary @ min CV:
#> -----------------------------------------------------
#> lasso-penalized linear regression with n=150, p=21
#> (At lambda=0.0023):
#> Nonzero coefficients: 7
#> Cross-validation error (deviance): 0.07
#> R-squared: 0.62
#> Signal-to-noise ratio: 1.64
#> Scale estimate (sigma): 0.267
#>
#> SR information:
#> Vartype Total Selected Saturation Penalty
#> Main effect 6 2 0.333 2.45
#> Order 1 interaction 12 3 0.250 3.46
#> Order 2 polynomial 3 2 0.667 3.00
#>
#>
#> Model summary @ CV1se:
#> -----------------------------------------------------
#> lasso-penalized linear regression with n=150, p=21
#> (At lambda=0.0074):
#> Nonzero coefficients: 6
#> Cross-validation error (deviance): 0.08
#> R-squared: 0.57
#> Signal-to-noise ratio: 1.35
#> Scale estimate (sigma): 0.284
#>
#> SR information:
#> Vartype Total Selected Saturation Penalty
#> Main effect 6 2 0.333 2.45
#> Order 1 interaction 12 2 0.167 3.46
#> Order 2 polynomial 3 2 0.667 3.00
par(mfrow = c(2,1), mar = c(4, 4, 3, 1))
plot(srl, plot_type = "both")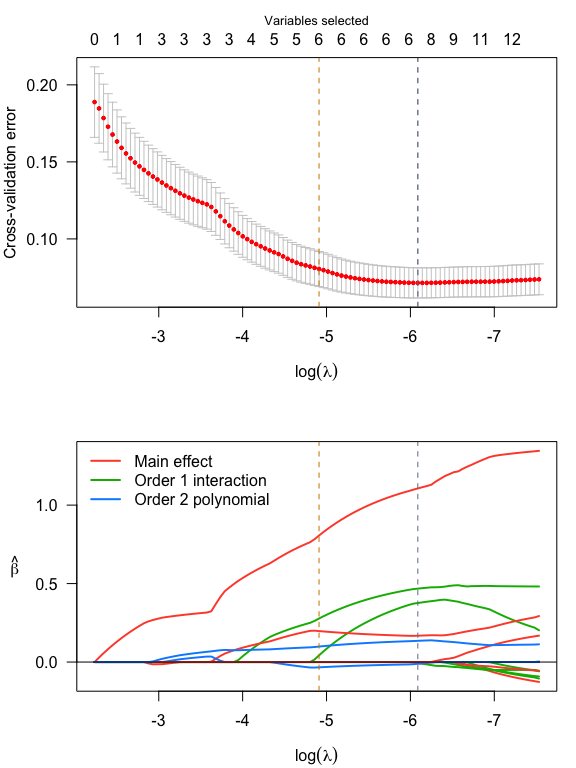
summary(srl, at = "cv1se")
#> lasso-penalized linear regression with n=150, p=21
#> At lambda=0.0074:
#> -------------------------------------------------
#> Nonzero coefficients : 6
#> Expected nonzero coefficients: 1.22
#> Average mfdr (6 features) : 0.204
#>
#> Estimate z mfdr Selected
#> Species_setosa 0.80638 18.013 < 1e-04 *
#> Sepal.Length_poly_1 0.19734 9.713 < 1e-04 *
#> Petal.Width_poly_2 0.09871 4.614 0.0011579 *
#> Petal.Width:Species_versicolor 0.27739 3.259 0.1328700 *
#> Sepal.Length_poly_2 -0.03363 -2.804 0.3663287 *
#> Sepal.Length:Species_setosa 0.04275 2.190 0.7229428 *effect_plot(srl, "Petal.Width", by = "Species", at = "cv1se", legend_location = "topright")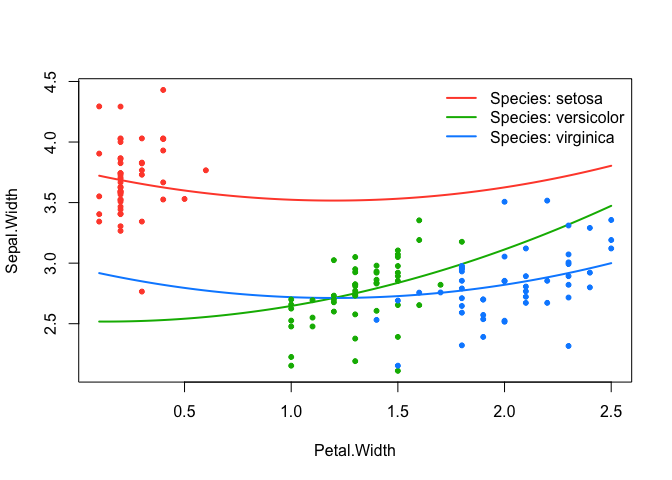
For more examples and a closer look at how to use this package, check out the package website.
Many thanks to the authors and maintainers of ncvreg and recipes.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.