The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

univariateML
is an R-package for user-friendly maximum likelihood
estimation of a selection
of parametric univariate densities and probability mass functions. In
addition to basic estimation capabilities, this package support
visualization through plot and qqmlplot, model
selection by AIC and BIC, confidence sets
through the parametric bootstrap with bootstrapml, and
convenience functions such as the density, distribution function,
quantile function, and random sampling at the estimated distribution
parameters.
Use the following command from inside R to install from
CRAN.
install.packages("univariateML")Or install the development version from Github.
# install.packages("devtools")
devtools::install_github("JonasMoss/univariateML")The core of univariateML are the ml***
functions, where *** is a distribution suffix such as
norm, gamma, or weibull.
library("univariateML")
mlweibull(egypt$age)
#> Loading required package: intervals
#> Maximum likelihood estimates for the Weibull model
#> shape scale
#> 1.404 33.564Now we can visually assess the fit of the Weibull model to the
egypt data with a plot.
hist(egypt$age, freq = FALSE, xlab = "Mortality", main = "Egypt")
lines(mlweibull(egypt$age))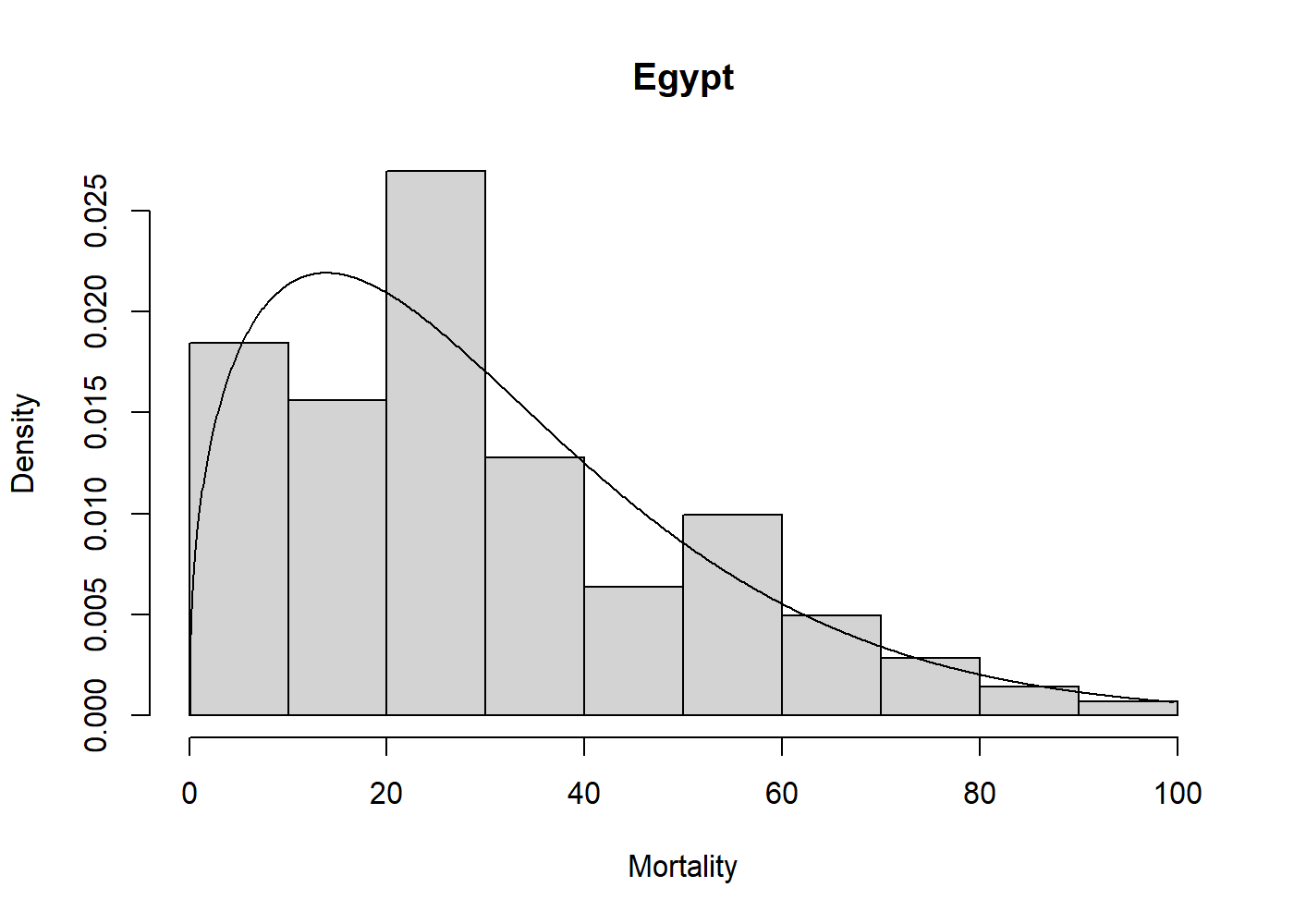
| Name | univariateML function | Package |
|---|---|---|
| Cauchy distribution | mlcauchy |
stats |
| Gumbel distribution | mlgumbel |
extraDistr |
| Laplace distribution | mllaplace |
extraDistr |
| Logistic distribution | mllogis |
stats |
| Normal distribution | mlnorm |
stats |
| Student t distribution | mlstd |
fGarch |
| Generalized Error distribution | mlged |
fGarch |
| Skew Normal distribution | mlsnorm |
fGarch |
| Skew Student t distribution | mlsstd |
fGarch |
| Skew Generalized Error distribution | mlsged |
fGarch |
| Beta prime distribution | mlbetapr |
extraDistr |
| Exponential distribution | mlexp |
stats |
| Gamma distribution | mlgamma |
stats |
| Inverse gamma distribution | mlinvgamma |
extraDistr |
| Inverse Gaussian distribution | mlinvgauss |
actuar |
| Inverse Weibull distribution | mlinvweibull |
actuar |
| Log-logistic distribution | mlllogis |
actuar |
| Log-normal distribution | mllnorm |
stats |
| Lomax distribution | mllomax |
extraDistr |
| Rayleigh distribution | mlrayleigh |
extraDistr |
| Weibull distribution | mlweibull |
stats |
| Log-gamma distribution | mllgamma |
actuar |
| Pareto distribution | mlpareto |
extraDistr |
| Beta distribution | mlbeta |
stats |
| Kumaraswamy distribution | mlkumar |
extraDistr |
| Logit-normal | mllogitnorm |
logitnorm |
| Uniform distribution | mlunif |
stats |
| Power distribution | mlpower |
extraDistr |
| Gompertz distribution | mlgompertz |
extraDistr |
| Burr distribution | mlburr |
actuar |
| Inverse Burr distribution | mlinvburr |
actuar |
| Birnbaum-Saunders | mlfatigue |
extraDistr |
| Name | univariateML function | Package |
|---|---|---|
| Poisson distribution | mlpois |
stats |
| Negative binomial distribution | mlnbinom |
stats |
| Binomial distribution | mlbinom |
stats |
| Geometric distribution | mlgeom |
stats |
| Zipf distribution | mlzipf |
sads |
| Zero-inflated Poisson distribution | mlzip |
extraDistr |
| Discrete uniform distribution | mldunif |
extraDistr |
| Logarithmic series distribution | mldunif |
extraDistr |
Analytic formulae for the maximum likelihood estimates are used
whenever they exist. Most ml*** functions without analytic
solutions have a custom made Newton-Raphson solver. These can be much
faster than a naïve solution using nlm or
optim. For example, mlbeta has a large speedup
over the naïve solution using nlm.
# install.packages("microbenchmark")
set.seed(313)
x <- rbeta(500, 2, 7)
microbenchmark::microbenchmark(
univariateML = univariateML::mlbeta(x),
naive = nlm(function(p) -sum(dbeta(x, p[1], p[2], log = TRUE)), p = c(1, 1))
)
#> Unit: microseconds
#> expr min lq mean median uq max neval
#> univariateML 201.4 244.05 349.978 365.6 422.2 791.9 100
#> naive 8289.4 8652.60 9170.378 8915.3 9288.0 18723.0 100The maximum likelihood estimators in this package have all been
subject to testing, see the tests folder for details.
For an overview of the package and its features see the overview vignette. For an illustration of how this package can make an otherwise long and laborious process much simpler, see the copula vignette.
Please read CONTRIBUTING.md for details about how to
contribute or get help.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.