
The hardware and bandwidth for this mirror is donated by METANET, the Webhosting and Full Service-Cloud Provider.
If you wish to report a bug, or if you are interested in having us mirror your free-software or open-source project, please feel free to contact us at mirror[@]metanet.ch.

The goal of wideRhino is to enable the construction of
canonical variate analysis (CVA) biplots for high-dimensional data
settings, specifically where the number of variables (\(p\)) exceeds the number of observations
(\(n\)). The package addresses the
singularity limitation of the within-group scatter matrix by leveraging
the generalised singular value decomposition (GSVD).
You can install the development version of wideRhino from GitHub with:
# install.packages("pak")
pak::pak("RaeesaGaney91/wideRhino")When \(p < n\), then the CVA-GSVD
biplot will result to the standard CVA biplot. Here is an example using
the penguins data:
library(wideRhino)
Penguins <- datasets::penguins[stats::complete.cases(penguins),]
CVAgsvd(X=Penguins[,3:6],group = Penguins[,1]) |>
CVAbiplot(group.col=c("blue","purple","forestgreen"))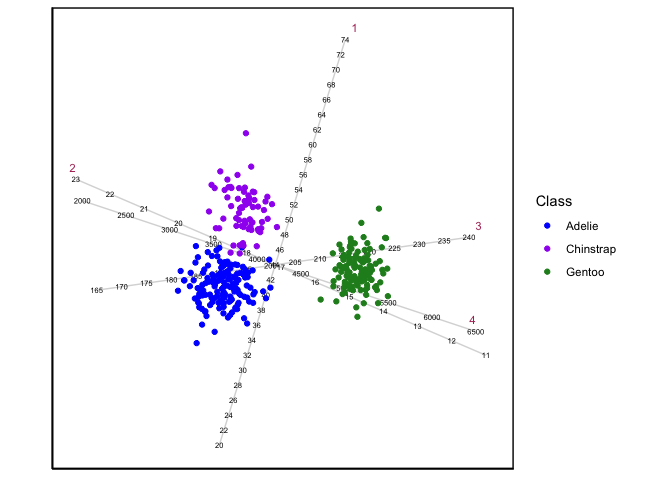
When \(p > n\), then the standard CVA biplot will not work due to the singularity of the within-scatter matrix, and this is when the GSVD becomes useful. Using a simulated data set with 3 groups, 100 observations and 300 variables, a CVA-GSVD biplot can be constructed:
data(sim_data)
CVAgsvd(X=sim_data[,2:301],group = sim_data[,1]) |>
CVAbiplot(group.col=c("tan1","darkcyan","darkslateblue"),which.var = 1:10,zoom.out=80)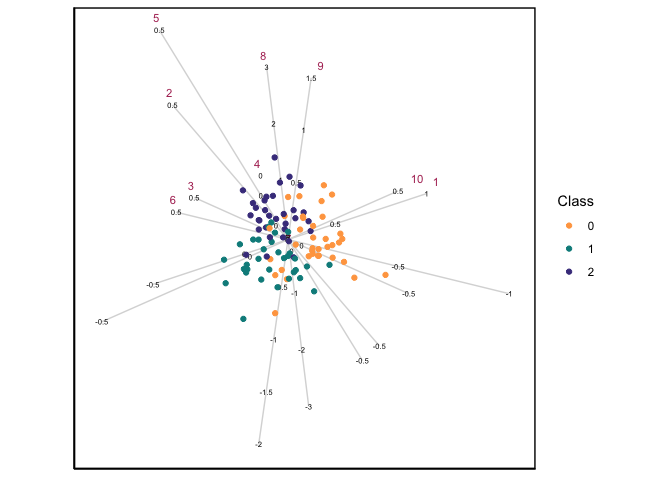
The name wideRhino is inspired by the white rhinoceros,
a species distinguished by its wide mouth and short legs. This physical
structure reflects the statistical characteristics of the data the
package is designed for: wide data with a large number of variables
(\(p\)) and a small number of
observations (\(n\)) — a setting often
described as “large \(p\), small \(n\)”.
Just as the white rhino’s wide frame is well-adapted to its environment, wideRhino is purpose-built for the challenges of high-dimensional multivariate analysis. By leveraging the generalised singular value decomposition (GSVD), it allows users to construct canonical variate analysis (CVA) biplots even when classical assumptions break down.
These binaries (installable software) and packages are in development.
They may not be fully stable and should be used with caution. We make no claims about them.